Logarytmy i funkcja wykładnicza Michał: Dobry wieczór forumowicze, mam kilka ptań z logarytmów i funkcji wykładniczej Jesli znazłby się ktoś chętny do pomocy będe bardzo wdzięczny za wytłumaczenie... Ok do rzeczy.

	|log |x||
1. f(x)=
	log |x|

ja to rozpisałem z definicji x x>=0 log x log x>=0 ⇔ x>=1 x { log x { −x x<0 −log x log x<0 ⇔x <1 No i co dalej? jak to podstawiac? Ile warunkow zrobić? :X Help me pls. 2.Rozwiąż nierówność (0,4)^3x+2 > 2,5 Ja to rozbijałem 0,4³x * 0,4² >2,5 teraz 0,4² na druga strone.... Ale to nic mi nie daje wychodzi 0,4³x > 15,(...) co z tym ? 3.Jak wyznaczyc największe wartości funkcji f jeżeli mmay jakiś konkretny przedział, niby wiem co i jak ale nie wiem jak się do tego zabrać przykład f(x)=log₃ (x+4) + log₃ (2−x), <−3;1> No to tyle Chyba na razie Prosze o pomoc wszystkich mających czas dla zagubionych duszyczek w świecie liczb Pozdrawiam i życzę udanej nocy/wieczoru .

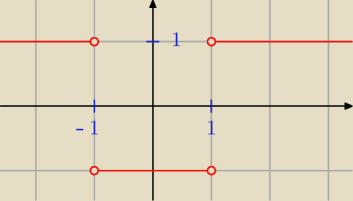Jack: 1. założenie: log|x| ≠ 0 −−> |x| ≠ 1 −−> x ≠ −1, x ≠ 1 log|x| > 0 −−> log|x| > log 1 −−> |x| > 1 −−> x ∊ (−∞;−1) U (1;∞) log|x| < 0 −−> log|x| < log 1 −−> |x| < 1 −−> x ∊ (−1;1) zatem dla x < −1

	|log|x||		log|x|
f(x) =		=		= 1
	log|x|		log|x|

dla x ∊ (−1;1)

	|log|x||		−log|x|
f(x) =		=		= − 1
	log|x|		log|x|

dla x > 1

	|log|x||		log|x|
f(x) =		=		= 1
	log|x|		log|x|

Jack: 2. (0,4)^3x+2 > 2,5

	4		25
(		)3x+2 >
	10		10

	2		5
(		)3x+2 >
	5		2

	2		2		2
(		)3x+2 > (		)−1 //jako, że		< 1 to zmieniam znak nierówności.
	5		5		5

3x + 2 < − 1 3x < − 3 x < − 1 x ∊ (−∞;−1)

Jack: 3. f(x) = log₃(x+4) + log₃(2−x), <−3;1> f(x) = log₃(x+4)+log₃(2−x) = log₃[(x+4)*(2−x)] = log₃(−x²−2x+8) Funkcja logarytm o podstawie 3 jest funkcją rosnącą (bo 3 > 1), jednakże argumentem funkcji jest funkcja kwadratowa (ramiona paraboli w dół) co za tym idzie? Największa wartość funkcji dla paraboli skierowanej w dół to jej wierzchołek.

	−b		2
p =		=		= − 1
	2a		−2

iksowa wierzchołka (czyli p) należy do dziedziny <−3;1> zatem liczymy jej wartość. f(−1) = log₃[−(−1)²−2*(−1)+8] = log₃(−1+2+8) = log₃9 = 2 możemy zbadać jeszcze wartości na krańcach przedziałów. f(−3) = log₃(−3+4) + log₃(2+3) = log₃(1) + log₃(5) = log₃(1*5) = log₃5 f(1) = log₃(1+4) + log₃(2−1) = log₃(5) + log₃(1) = log₃5 no i widać, że dla x = −1 mamy wartość największą, równą 2.

Michał: Oh yeah, dzięki Jack no genialnie to zrobiłeś choć nie do końca rozumiem podpunkt 3 Jednak stosując się do niego i postepując według Twoich wskazowek rozwiązałem poprawnie wszystkie poprzednie przykłady. Myślę że mój brak zrozumienia dla tego wynika z braku wiedzy elementarnej na temat funkcji kwadratowej (problem z zrozumieniem czemu bierzemy najwieksza wartosc z wykresu i czemu licze p X_x, podejrzewam że piszac wierzchołek miałes na mysli własnie "p" no nic muszę sobie poprzypominac jak to szło)... Raz jeszcze dzięki Jack BARDZO DZIĘKI −−−−−−−−−−−−−− Robiłem też inne zadnka z tych, tematów i mam parę pytań nowych, pozwolę sobie je tu wypisać i proszę ponownie o wytłumaczenie czemu tak a nie inaczej: 1. log₂ x+ 2√log₂ x=8 podstawiam t=√log₂ x wychodzi delta 36 i miejsca zerowe −4 i 2 z 2 po podstawieniu za logarytm wychodzi 16 (prawidłowa odp) drugi pierwiastek całkowicie pominięto w odp. Według mojego rozumowania pomijamy go bo t>=0 Pytanie dla czego ma byc t>=0, nigdy nie stawiałem tego warunku przy log jak podstawiałem t robiłem to tylko w funkcji wykładniczej Jak to w koncu jest z tym założeniem i co ono zakłada ? 2. Z funkcji wykładniczej 8^x−4^x+0,5−2^x+2=0 t=2^x t>0 t³−2t²−t+2 t²(t−1)−t+2 <−− chyba dobrze wyliczone no i co z tym teraz przeciez nie mam wspolnych czynników Takie oto dwa przykłady jakbyście mogli pomóc będę wdzieczny i doceniam kazda chęc pomocy także z góry dzięki. PS, Pozdrawiam Michał

Eta: 2/ t³−2t²−t+2=0 t²(t−2)−(t−2)=0 (t−2)(t²−1)=0 (t−2)(t−1)(t+1)=0 i t>0 zatem t=2 v t=1 2^x=2 v 2^x=1 x=1 v x=0 ==========

Michał: Ok Dzięki eto to drugie jest już jasne, szczerze to myslałem nad tym czy tak mogłbym zrobić ale mysalem ze jak wywlae minus przed nawias to będzie −(−t−2) :X. No nie wiem skąd takie głupie pomysły dziękuję za pomoc z drugim przykładem

Jack: zad1. mamy log₂x zatem założenie co do logarytmu: x > 0 podstawiasz t = √log₂x, zatem t ≥ 0 dlaczego tak? a ile wynosi √−4 ? albo √−2? nie wiesz. Znamy tylko pierwiastki z liczb nieujemnych, dlatego to co jest pod pierwiastkiem musi być nieujemne czyli ≥ 0 (w szkole średniej nie znamy ujemnych, na studiach to się zmieni) ale póki co, to co jest pod pierwiastkiem nie może być ujemne.

Michał: Oki :X czyli jak dobrze rozumie jezeli bede miął √x w zadaniu to musze załozyc ze √x>=0 EH takie oczywiste, a nie pomysalem o tym... A sytuacja, gdyby podstawił np za log₂ x= t to wtedy założenie ze t>=0 nie jest już potrzebne?

Eta: tylko x>0 , wartości logarytmu t∊R

Michał: Ok dziękuję eta dzięki Jack, życzę wam udanej nocy dobranoc