zad help s: Iloczyn trzech kolejnych liczb całkowitych jest 6 razy większy od kwadratu najmniejszej z tych liczb powiększonego o 1. Wyznacz te liczby.

Jerzy: (k − 1)*k*(k +1) > 6[(k − 1)² + 1] i k > 0

s: dlaczego nie x(x+1)(x+2)=6(x²+6)

kochanus_niepospolitus: jak już to x(x+1)(x+2) = 6(x² +1) i wtedy oba równania przedstawiają dokładnie to samo

kochanus_niepospolitus: no i ma być nierówność

Jerzy: Możesz tak, tylko popraw prawą stronę , a u mnie założenie k > 0 jest niepotrzebne.

s: dzieki mam 1 w zeszycie a napisałam 6 A takie zadanie Wyznacz wszystkie wartości parametru k, dla których równanie k²x−1=x(3k−2)−k ma rozwiązanie w zniorze liczb rzeczywistych

s: *zbiorze

Jerzy: Najpierw oblicz x

kochanus_niepospolitus: x(k² − 3k + 2) + k−1 = 0 to równanie będzie miało rozwiązanie gdy: k² − 3k + 2 ≠0

s: jak ?

s: A co jesli wczesnie robiłem te zadania a teraz jakos zapomniałem , to znaczy ,że potrzebuje odpoczynku ? doda ,że mało spie

Jerzy:

	1 − k
x =
	k2 − 3k + 2

Dla: k = 2 − brak k ≠ 2 i k ≠ 1 − jedno rozwiazanie k = 1 tożsamość

s: A ktoś coś do mojego koment ?

Jerzy: Nie mam zwyczaju komentować bredni.

s: Dzieki Uzasadnij, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność |x+5|+|x−2|>=7

s: wynik jesli można mi wyszło xe <2;∞)

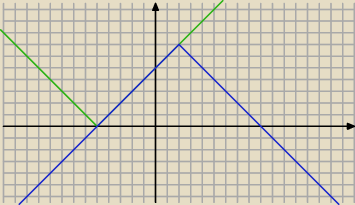
Jerzy: Zielona: f(x) = |x + 5| Niebieska: g(x) = − |x − 2| + 7

Jerzy: To źle ci wyszło, bo x ∊ R