zad matthew: mam takie zadanie:

	1
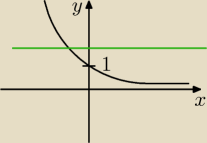
Narysuj wykres funkcji f(x) = (		)x+|x| i na podstawie wykresu określ liczbę rozwiązań
	3

równania f(x) = m, w zależności od parametru m. Nie wiem czy rysunek jest dobrze wykonany... "m" ma jedna rozwiazanie, gdy m>0 "m" nie ma rozwiazań, gdy m<0 Proszę o pomoc Dziekuje

Bogdan: Rysunek i rozwiązanie nie jest poprawne, rozpatrz przypadki; x < 0, x ≥ 0.

matthew: nie wiem....

	1
dla x <0 f(x) = (		)−x−x = 32x ? − kolor zielony
	3

	1
dla x ≥ 0 f(x) = (		)2x ?
	3

dla m (0,1) ∪ (1, +∞) dwa rozwiazania dla m = 1 jedno rozwiazanie dla m ≤ 0 brak rozwiazań bardzo prosze o sprawdzenie...

matthew: prosze o pomoc...

Bogdan:

	1
Dla x < 0: f(x) = (		)x − x = 1
	3

	1		1
Dla x ≥ 0: f(x) = (		)x + x = (		)2x
	3		3

matthew: No wlasnie zastanawialem sie nad ta jedynką... ale w takim razie jak mam narysowac jego wykres? A czy odpowiedzi dla parametru m sformulowalem dobre...? Dziekuje za odpowiedz

matthew: Tzn. ze rysuje wykres tylko funkcji dla ktorej x ≥ 0?

matthew: mam jeszcze takie zadanie:

	tgx
Dana jest funkcja f(x) =		dla x∊<−π, π>
	|tgx|

a) zapisz wzór tej funkcji bez użycia wartości bezwzględnej b) Naraysuj wykres funkcji f c) rozwiąż nierówność f(x) <0

matthew: nie wiem czy dobrze, ale w punkcie a) bedzie chyba tak:

	tgx
f(x) =
	|tgx|

dla tgx < 0

	tgx
f(x) =		= −1
	−tgx

dla tgx ≥ 0

	tgx
f(x) =		= 1
	tgx

Bardzo prosze o sprawdzenie

Anna: Dobrze, tylko : dla tgx> 0 ( mianownik nie może być zerem).

matthew: Anna, a możesz sprawdzic to poprzednie zadanie... wlasciwie tam trzeba narysowac juz tylko wykres ale nie jestem pewien jak... Bogdan napisal, ze w pierwszym przypadku f(x) = 1 .. ale nie wiem jak przedstawic to na rysunku... prosze o pomoc Dziekuje za odpowiedz

matthew: w punkcie b) bedzie tak? kolor zielony f(x) = 1 kolor czerwony f(x) = −1

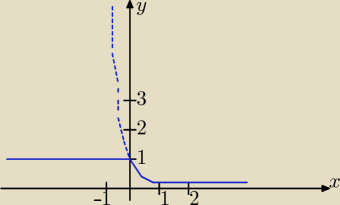
Anna: Wykresem jest linia ciągła.

	1
x 0 1 −1 −
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1
y 1		9 3
	9

matthew: Dziekuje A wiesz może jak zrobic trzeci podpunkt c) w ostatnim zadaniu?

Anna: Robię Ci nowy wykres do zad. z tangensem, gdyż Twój jest niepoprawny.

Anna:

	π		π
c) f(x) < 0 ⇔ x ∊ (−		, 0) ∪ (		, π)
	2		2