Uniform continuous distribution - prawdopodobienstwo ze x<3. Ktos pomoze? Natalia: Podana jest funkcja: f(x) = (x−1)/8, 1<x<5. Ktora jest density function dla X. a.) Graph the density function. Narysuj wykres − narysowalam ladnie wykres funkcji liniowej f(x)=1/8x−1/8. b.) Find the probability that X lies between 2 and 4. Znajdz prawdopodobienstwo ze x lezy miedzy 2 a 4. Jako, ze a=1, b=5, a pdf dla uniform distribution to f(x)=1/(b−a)=1/4 Jako prawdopodobienstwo to pole pod wykresem: P(2<x<4)=(4−2)*1/4=1/2 Co zgadza sie z odpowiedziami. c.) What is the probability that X is less than 3? Prawdopodobienstwo ze X jest mniejsze niz 3. Jak zabralam sie za ten podpunkt: P(x<3)=P(1<x<3)=(3−1)*1/4=1/2 Natomiast w odpowiedziach jest napisane, ze wynik ma byc 1/4. Ktos ma pomysl jak sie za to zabrac, co robie zle? Moze trzeba przeksztalcic jakos poczatkowa funkcje? Bede baardzo wdzieczna. Pozdrawiam

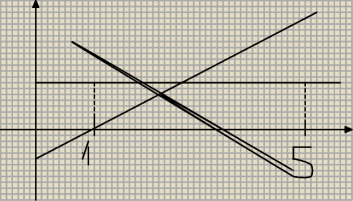
Natalia: Tak mniej wiecej wyglada wykres (bez tego bochomaza od 5 − nie wyszlo mi cos)

Adamm: b)

	f(2)+f(4)
P(2<X<4)=		*(4−2)=1/2
	2

c)

	1
P(X<3)=		*(3−1)*f(3)=1/4
	2