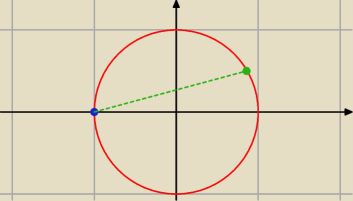
geometria różniczkowa sss: napisz równania parametryczne okręgu x²+y²=a² przyjmując za parametr t współczynnik kierunkowy cięciwy okręgu przechodzącej przez punkt (−a,0)

Adamm: trochę za mało danych o tej cięciwie

sss: to cała treść zadania z książki elementy geometrii różniczkowej z zadaniami Gdowskiego

sss: mam tez odpowiedz ale kompletnie nie wiem skąd to się bierze

Adamm: słuchaj wiemy tylko że to cięciwa i ma jeden punkt wspólny z tym okręgiem tak naprawdę nic nie wiemy, jest mnóstwo takich cięciw

sss: no właśnie wiem brakuje drugiego punktu przecięcia

sss: w odpowiedziach jest x= a(1−t²)/1+t² i y=2at/1+t²

Adamm:

	y
t=
	a+x

	a2−x2
t2=
	(a+x)2

	a−x
t2=
	a+x

	2a
t2+1=
	a+x

2a
	=x+a
t2+1

a(1−t2)
	=x
t2+1

y=t(a+x)=U{2at{t²+1} nie zrozumiałem treści

Adamm:

	2at
y=
	t2+1

sss: nie rozumiem czemu t=y/a+x pomożesz?

Adamm: t to Δy/Δx Δy to y−0=y Δx to x−(−a)=x+a

sss: dzięki !