Wzór de Moivre'a - wyjaśnienie esendo: 2⁵⁰ (cos175π + i sin175π) = 2⁵⁰ (cosπ + i sinπ) = 2⁵⁰ (−1 + i*0) Nie rozumiem dlaczego 175 znika. W każdym podobnym przykładzie całe liczby zawsze znikają, a zostają tylko ułamki. Chciałbym jeszcze zrozumieć dlaczego cosπ zamienia się na −1, a sinπ na 0.

' Leszek: Zastosuj wzory redukcyjne : np. cos 175π = cos ( 174 π + π) = cos π cos π = −1 , popatrz na wykres funkcji y = cos x , Analogicznie dla sin α ,

Ariel: Obie funkcje sa okresowe o okresie 2π cos175π= cos(2*77π+π)= cosπ

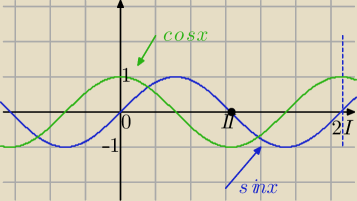
Mila: y=sinx i y= cosx to funkcje okresowe, T=2π cos(174π+π)=cos(π+87*2π)=cos(π)

esendo: Teraz już wszystko jasne. Nie wiedziałem, że chodzi o wartości z wykresów sinusa i cosinusa.