funkcja kwadratowa, parametr m Paweł: Podaj wszystkie wartości parametru m, dla których równanie |x² − 6x + 5| +m − 2 = 0 ma dokładnie dwa dodatnie rozwiązania. Mam wykres funkcji f(x) = |x² − 6x + 5| − 2, więc dla parametru m 2 rozwiązania dodatnie są w przedziale (−6;−7) oraz dla 2. Tak więc −m∊(6;7)∪{−2} Odpowiedź jednak jest inna, czyli (−3;−2)∪{2}. W czym problem? Miejsca zerowe: 1,5. Wierzchołek paraboli: (3;6). Punkt przecięcia z osią OY: (0;7).

Paweł: w przedziale (6;7) i dla 2, więc −m∊(−6;−7)∪{−2} (mała pomyłka)

'Leszek: Zrob starannie wykres funkcji f(x) i przesuwaj poziomo linijke y = − m do przeciecia z wykresem ( nie zgub tego ( − ) ) ! !

Paweł: No własnie tak zrobiłem i jakoś nie wychodzi. Kilkukrotnie sprawdzałem, czy wykres jest poprawny, ale wiadomo, mogłem i tak gdzieś błąd popełnić. Prosiłbym bardzo o prześledzenie zadania (jeśli ma pan czas), abym mógł zauważyć swoją pomyłkę.

Paweł: Okej, problem rozwiązany. Źle przesunąłem wykres funkcji.

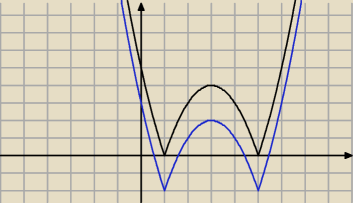
Ariel: y=|x²−6x+5| czarny kolor y=|x²−6x+5|−2 kolor niebieski Narysowane masz dwa wykresy bo nie wiem czy robiles to a) |x²−6x+5|= 2−m wtedy wykres czarny b) czy |x²−6x+5|−2=−m wtedy wykres niebieski

Paweł: Narysowałem wykres niebieski, lecz przesunąłem o dwa w górę (chwilowe zaćmienie mózgu). Dziękuję mimo wszystko za rozrysowanie i życzę miłego wieczoru. (:

Ariel: Musisz zobaczyc tez to ze jesli robiles s[posobem b) wykres niebieski to dla m=−2 masz prosta o rownaniu y=−(−2)=2 a wtedy masz 3 rozwiazania dodatnie . wiec ?

'Leszek: Lepiej zrobic bylo wykres funkcji g(x) = | x² − 6x +5 | i nastepnie znajdujemy punkty przeciacia wykresu z y = 2−m

Ariel: Moj blad . Juz slepne tam bylo w rozwiazaniu suma 2 a nie (−2)