Rysowanie funkcji wykładniczej SEKS INSTRUKTOR: Jak narysować funkcję f(x) = 2^x−1 + 2^−x+1 przekształciłem to tak f(x) = 2^x−1 + 2^−(x−1) i nie wiem co dalej z tym zrobić f(x) = 2^x−1 + ¹₂^x−1

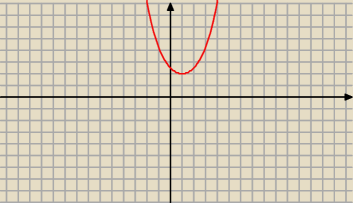
Adamm: zauważ, że ta funkcja to g(x)=2^x+2^−x przesunięta o wektor [1; 0] po drugie, g(x)=g(−x) (funkcja jest parzysta) po trzecie, g'(x)=ln2*(2^x−2^−x) (funkcja osiąga jedyne ekstremum dla x=0, dla x>0 rośnie) po czwarte, g''(x)=ln²2(2^x+2^−x) (funkcja jest wypukła) z tymi informacjami, już łatwo narysować wykres

SEKS INSTRUKTOR: jak widzę, to ten wykres sugeruje, że jest to wykres funkcji kwadratowej, czy za pomocą rozpisania wzoru f(x) da się jakoś do niego dojść?

Adamm: to nie jest wykres funkcji kwadratowej, po prostu ma wiele własności które funkcja kwadratowa też posiada (parzystość, najpierw maleje a potem rośnie, wypukłość)

SEKS INSTRUKTOR: Czyli żeby ją narysować w najprostszy sposób, należy podstawiać kolejne wartości całkowite?

Adamm: tak, i łączysz linią, ale zaokrągloną w dół (bo funkcja jest wypukła)