matematykaszkolna.pl
Granica w punkcie Almin: zbadaj granice w punkcie x=0, f(x)=x+|x|2x
12 paź 17:14
Blee: No to licz granice lewo i prawostronna ... w czym problem?
12 paź 17:40
Almin: Nie wychodzi mi, ponieważ zawsze dziele przez zero i nie wiem jak postąpić z tą wartością bezwzględną
12 paź 17:56
Almin: Czy ktoś mógłby to rozpisać? Byłbym bardzo wdzięczny
12 paź 18:13
Mila: rysunek
 1 |x| 
f(x)=
+
 2 2x 
|x|=x dla x>0 |x|=−x dla x<0
 1 |x| 1 −x 1 1 
limx→0−(
+
)=limx→0−(
+
)=
−
=0
 2 2x 2 2x 2 2 
 1 |x| 1 x 1 1 
limx→0+(
+
)=limx→0+(
+
)=
+
=1
 2 2x 2 2x 2 2 
12 paź 18:39
3Silnia&6:
 x(1+sgnx) 1+sgnx 
f(x) =
=
 2x 2 
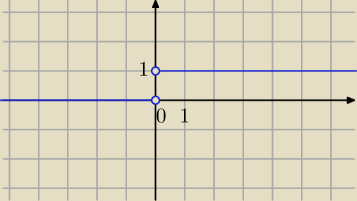
f(x) → 0 dla x → 0− f(x) → 1 dla x → 0+ granica nie istnieje
12 paź 18:40