Kombinatoryka beginneritstudent: Na ile różnych sposobów można rozsadzić n osób wokół okrągłego stołu z n+w miejscami?

Jerzy: Wybieramy n miejsc spośród n + w i permutujemy osoby:

n+w n
	*n!

beginneritstudent: Mi wyszło (n+w−1)*(n+w−2)*...*(w+1), a to chyba nie to samo co napisałeś. Pierwsza obojętnie jakie miejsce wybierze, druga ma (n+w−1) wyborów i tak dalej aż do ostatniej, która ma w+1 wyborów. Właśnie nie wiem czy dobrze myślę, mógłbyś bliżej wytłumaczyć swoje rozwiązanie i mnie poprawić jak coś?

Jerzy: Niech: n = 2 w = 1 n + w = 3 Mamy trzy miejsca i dwie osoby. Sprawdź na ile sposobów je mozna posadzić, a potem podstaw te dane do mojego i Twojego wzoru i zobaczysz , który da dobry wynik.

beginneritstudent: No w takiej sytuacji tylko dwie możliwości, czyli chyba mój jest bliższy... I'm confused

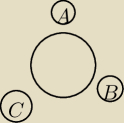
Jerzy: Możliwości jest 6 3 wybory dwóch miejsc: (A,B) (A,C) (B,C) i na kazdym wyborze zamiana miejsc (*2) 3*2 = 6

beginneritstudent: A no tak, ale mi raczej chodzi o taką sytuację, że liczy się kto koło kogo siedzi, czyli w tym przypadku powiedzmy Janek sobie siądzie i potem Tomek może usiąść po jego lewej albo prawej, więcej opcji nie ma w takim założeniu

Jerzy: Popatrz na rysunek. Janek siada na A , a Tomek na B. Ale innym zdarzeniem dla tych dwóch miejsc jest: Tomek siada na A , a Janek na B

beginneritstudent: No tak i to są jedyne dwa zdarzenia, bo zakładamy, że miejsca są nienumerowane, nierozróżnialne

Jerzy: Jak to dwa ? Przecież mogą usiąść równie dobrze na krzesłach B i C lub A i C