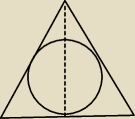
 Witam. Potrzebuje pomocy w zadaniu. Okrąg o promieniu 1 cm jest wpisany w trójkąt równoramienny
o podstawie 4 cm. Oblicz długość ramienia tego trójkąta.
Próbowałem zrobić to zadanie już ze 100 razy ale wychodzi mi że a=2√2 a w odpowiedziach jest
3 i 1/3
i sporządziłem do niego taki rysunek : https://zapodaj.net/404232f509119.jpg.html
Witam. Potrzebuje pomocy w zadaniu. Okrąg o promieniu 1 cm jest wpisany w trójkąt równoramienny
o podstawie 4 cm. Oblicz długość ramienia tego trójkąta.
Próbowałem zrobić to zadanie już ze 100 razy ale wychodzi mi że a=2√2 a w odpowiedziach jest
3 i 1/3
i sporządziłem do niego taki rysunek : https://zapodaj.net/404232f509119.jpg.html
| 1 | ||
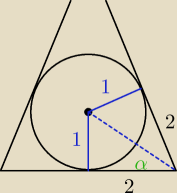
tg α = | −> 2sinα = cosα | |
| 2 |
| 1 | √5 | |||
sinα = | = | |||
| √5 | 5 |
| 2 | |
= cos(2α) = cos2α − sin2α = 3sin2α ⇔ | |
| b |
| 2 | 2 | 10 | ||||||||||
⇔ b = | = | = | ||||||||||
| 3sin2α |
| 3 |
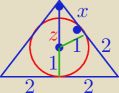 z2 = 1 + x2 z > 1
Z podobieństwa trójkątów prostokątnych mamy
z2 = 1 + x2 z > 1
Z podobieństwa trójkątów prostokątnych mamy
| 1 | 2 | ||
= | ⇒ 2 z = x + 2 ⇒ x = 2 z − 2 | ||
| z | x + 2 |
| 8 − 2 | ||
z = | = 1 − odpada | |
| 6 |
| 5 | ||
lub z = | ||
| 3 |
| 25 | 9 | 16 | ||||
x2 = z2 − 1 = | − | = | ||||
| 9 | 9 | 9 |
| 4 | ||
x = | ||
| 3 |
| 4 | 1 | |||
x + 2 = | + 2 = 3 | |||
| 3 | 3 |

| sin | ||
tg= | ||
| cos |
| sin | 1 | ||
= | to .... | ||
| cos | 2 |

| 2P | ||
r= | , 2P= 4√b2−4 , b>2 | |
| 2b+4 |
| 1 | ||
3b2−4b−20=0 ⇒ b=3 | ||
| 3 |
