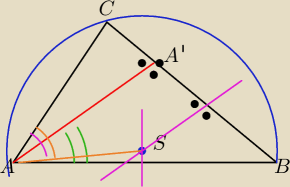
Katy w kole nocnaćma: Niech AA' bedzie wysokoscia trojkata ostrokatnego ABC a S srodkiem okregu iopsanego na tym trojkacie Udowodnij ze kąt BAA' = ∡SAC

5-latek: Wiem z esrodek okregu opisanego na trojkacie lezy na przeciu sie symetralnych W czym mi to pomoze ?

iteRacja: <BAA' = 90^o − <CBA /z Δ prostokątnego BAA' <CSA = 2*<CBA / wpisany i środkowy oparte na tym samym łuku <SAC = <SCA / ΔSAC jest równoramienny − AS, AC promienie

	1		1
<SAC =		(180o − <CSA) = 90o −		<CSA = 90o − <CBA
	2		2

<SAC = <BAA' i koniec..

5-latek: dziekuje Mialem wlasnie pisac ze ∡SAC = ∡BAC jako wpisane oparte na tym samym luku AC Za trudne zadania

5-latek: iteRacjo Moj problem polega na tym ze potrafie od razu zobaczyc jakies katy , ale jesli przyjdzie znalez go gdy trzeba np jakies dodac czy odjac o juz tego nie widze . Moze sie poprawi gdy bede przerabial podobienstwo trojkatw i Tw talesa .

iteRacja: zadania nie są za trudne dla Ciebie! naprawdę dużo ich rozwiązujesz, a to zawsze dobrze się kończy podstawa to dobry rysunek : właściwy bardzo pomaga, zły jeszcze bardziej przeszkadza na tym są zniekształcone kąty i Δ za bardzo zbliżony do prostokątnego do rysunków warto ściągnąć Geogebrę, szybko się rysuje, łatwo jest coś poprawić

iteRacja: to jeszcze jedna rzecz: ∡SAC = ∡BAC jako wpisane oparte na tym samym luku AC te kąty nie są oparte na tym samym łuku, czy rzeczywiście o te chodziło?

5-latek: Przepraszam jestem jeszcze slaby i pozna reaguje Sa trudne w tym zbiorze . W zbiorze Drobka Szymanski do geometrii w tym dziale sa latwiejszse chyba nie o to chodzi bo jesli bym chcial tak napisac to musialbym poprowadzic prosta AD np przechodzaca przez punkt S i wtedy kat DAC oparty = katowi BAC

iteRacja: te kąty DAC i BAC nie będą równe i nie będą oparte na tym samym łuku w Δ ostrokątnym (tylko w Δ prostokątnym będą, zrób kilka rysunków w ramach ćwiczeń) a z jakiego zbioru jest to zadanie?

5-latek: Juz odpisuje Matematyka w szkole sredniej Geometria Zbior zadan cz 1 Maria Małek GWO Gdansk 1993r