Ciągłość funkcji, granica funkcji Krystian: Witam, mógłby ktoś mi tutaj pomóc jak rozgryść te zadania? 1. Dla jakiej wartości parametru a funkcja f jest ciagła w punkcie x₀ ?

	x2−4x+4
f(x)=		dla x≠2
	x2−2x

a dla x=2 2. Oblicz granicę

	1−x
a) lim x→4+
	x−4

	x−6
b) lim x→5−
	5−x

Blee: Granice umiemy liczyc?

Blee: 2 a) − nieskonczonosc 2 b) − nieskonczonosc

Blee: 1) dla a=0

Krystian: Ale przecież po podstawieniu do mianownika jest 4−4=0 a nie można dzielić przez zero?

5-latek: Przeciez to nie jest dokladnie 4

Janek191:

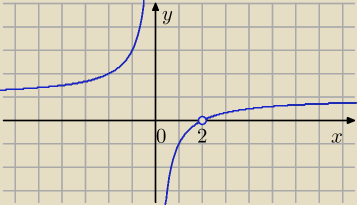
	( x − 2)2		x − 2
f(x) =		=
	x*(x −2)		x

	0
lim f(x) =		= 0
	2

x → 2 więc a = 0 =====

Krystian: Dzięki Nie pomyślałem o tym, żeby wyłączyć x przed nawias w mianowniku >,< Mam jeszcze coś takiego do rozwiązania: Dla jakich parametrów a i b funkcja f jest ciągła? Dla wyznaczonych parametrów a i b naszkicuj wykres tej funkcji i z wykresu odczytaj jej ekstrema. f(x)= (a−x)³ dla x<−1 = b dla x=−1 = 2(x−a) dla x>−1 Więc tutaj musi być (a−x)³=b=2(x−a)? 2(x−a)=(a−x)³ −2(a−x)=(a−x)³ /:(a−x) −2=(a−x)² −2=a²−2ax−x² Po podstawieniu −1: −2=a²+2a+1 0=a²+2+3 Ale delta wychodzi na minusie i nie wiem co mogę z tym zrobić

kochanus_niepospolitus: co do granic jednostronnych musisz to 'na chłopski' rozum zrozumieć, że: lim_x−>4⁺ x = 4.0000000000000000000000000000001 (czyli liczba odrobinę większa od 4, ale to jest 'nieskończenie mała odrobina' ) I wtedy

	2		2
limx−>4+		=		= +∞ bo to jest dodatnia stała przez
	4 − x		0.0000000000000000001

nieskończenie małą (dodatnią) wartość.

kochanus_niepospolitus: analogicznie granica lewostronna to będzie lim_x−>4⁻ x = 3.9999999999999999999999999999999999999999

Krystian: Aaa, zapomniało mi się o tym Pomoże ktoś z tym kolejnym? Dla jakich parametrów a i b funkcja f jest ciągła? Dla wyznaczonych parametrów a i b naszkicuj wykres tej funkcji i z wykresu odczytaj jej ekstrema. f(x)= (a−x)3 dla x<−1 = b dla x=−1 = 2(x−a) dla x>−1

kochanus_niepospolitus: lim_x−>−1⁻ f(x) = (a+1)³ f(−1) = b lim_x−>−1⁺ f(x) = 2(−1−a) i teraz: (a+1)³ = 2(−1−a) ⇔ a = −1 i wtedy lim_x−>−1 f(x) = 0 , więc b=0 Odp: Dla a = −1 i b = 0

kochanus_niepospolitus: może jeszcze Ci rozpisze: (a+1)³ = 2(−1−a) ⇔ (a+1)³ = −2(1+a) ⇔ (a+1)[ (a+1)² + 2] = 0 stąd jedyna wartość (w zbiorze liczb rzeczywistych) spełniająca to równanie to a = −1