Liczby zespolone, nierówność
Kamil: nie mam pojęcia jak się w ogóle za ten przkład zabrać z liczb zespolonych, chciałem coś zrobić
z dyskusja przypadków, próbowałem coś z interpretacją geometryczna, ale jedyne na co wpadłem
to jakaś elipsa która mógłbym spróbować stworzyć w oparciu o dwa punkty no ale nie o to pewnie
chodzi, a tutaj już daję przykład
|z+1|+|z−3i|<8
nie chodzi mi nawet o rozwiązanie tego, ale chociażby o jakieś naprowadzenie, pokazanie
pierwszego kroku, z góry dziękuję

9 paź 21:53
5-latek: A to nie bedzie wnetrze kola o srodku −1 +3i i promieniu √8 ?
Moge sie mylic
9 paź 21:56
Kamil: wnętrze koła chyba wtedy jak mielibyśmy wszystko pod jednym modułem liczby zespolonej
moglibyśmy rozpatrywać tak jak np w takim przypadku |z−(3+2i)|, z racji że to jest suma wydaje
mi się że nie mogę tak zrobić
9 paź 22:04
Kamil: O i przepraszam błąd w przykładzie |z+i|+|z−3i|<8 to jest dobry przykład
9 paź 22:04
PW:
||z+i| oraz |z−3| mierzą odległości liczby z od (0,−i) oraz od (3,0). Przypomnij sobie jak
się rysuje elipsę "metodą ogrodnika".
9 paź 22:15
Kamil: tylko czy takie rozwiazanie wystarczy, bo o to sie obawialem
9 paź 22:38
PW: Kiedy mamy |z−a|<5, to podajemy interpretację geometryczną: wnętrze koła o środku a i promieniu
5. Inaczej trudno odpowiedzieć na pytanie o rozwiązanie nierówności. Podobnie jest w tym
zadaniu − trzeba narysować elipsę, której wnętrze jest rozwiązaniem nierówności.
9 paź 22:48
Mila:
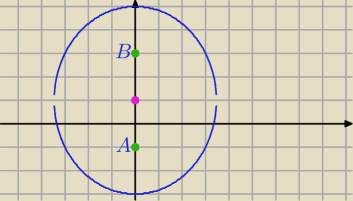
|z+i|+|z−3i|<8
Suma odległości od punktów
A=(0,−1) ,B=(0,3) jest mniejsza od 8
|AB|=4
to będzie wnętrze elipsy
ogniska : (0,−1), (0,3)
Półosie:
2a=8, a=4
odległość ogniskowa: 2c=4,c=2
c
2=a
2−b
2
4=16−b
2, b=2
√3
Można naszkicować
Albo tak
2) Po podstawieniu:
z=x+iy, x, y∊R można ustalić równanie, ale trudno doprowadzić do postaci kanonicznej
|x+iy+i|+|x+iy−3i|=8
√(x2+(y+1)2+
√x2+(y−3)2=8⇔
√x2+y2+2y+1=8−
√x2+y2−3y+9 /
2 po przekształceniach
9 paź 22:54
9 paź 22:55
Kamil: Dobrze dziękuję za pomoc
9 paź 23:52
Mila:

10 paź 00:02

 |z+i|+|z−3i|<8
Suma odległości od punktów
A=(0,−1) ,B=(0,3) jest mniejsza od 8
|AB|=4
to będzie wnętrze elipsy
ogniska : (0,−1), (0,3)
Półosie:
2a=8, a=4
odległość ogniskowa: 2c=4,c=2
c2=a2−b2
4=16−b2, b=2√3
Można naszkicować
Albo tak
2) Po podstawieniu:
z=x+iy, x, y∊R można ustalić równanie, ale trudno doprowadzić do postaci kanonicznej
|x+iy+i|+|x+iy−3i|=8
√(x2+(y+1)2+√x2+(y−3)2=8⇔
√x2+y2+2y+1=8−√x2+y2−3y+9 /2 po przekształceniach
|z+i|+|z−3i|<8
Suma odległości od punktów
A=(0,−1) ,B=(0,3) jest mniejsza od 8
|AB|=4
to będzie wnętrze elipsy
ogniska : (0,−1), (0,3)
Półosie:
2a=8, a=4
odległość ogniskowa: 2c=4,c=2
c2=a2−b2
4=16−b2, b=2√3
Można naszkicować
Albo tak
2) Po podstawieniu:
z=x+iy, x, y∊R można ustalić równanie, ale trudno doprowadzić do postaci kanonicznej
|x+iy+i|+|x+iy−3i|=8
√(x2+(y+1)2+√x2+(y−3)2=8⇔
√x2+y2+2y+1=8−√x2+y2−3y+9 /2 po przekształceniach
