s bc: Zbadaj monotoniczność funkjci (x−1) / (x−5) korzystając z definicji: x₁<2₂ x₁−x₂ < > 0 ..... obliczam : (x₁−1) / (x₁−5) − ( x₂−1)/(x₂−5) i co dalej bo nie wiem jak to doproawdzic do prostszej postaci

Bogdan:

	x − 1
f(x) =		, x ≠ 5
	x − 5

dla x < 5: Założenia: x₁ < 5 ⇒ x₁ − 5 < 0 i x₂ < 5 ⇒ x₂ − 5 < 0 i x₂ − x₁ > 0

	x2 − 1		x1 − 1
sprawdzamy znak różnicy: f(x2) − f(x1) =		−		=
	x2 − 5		x1 − 5

	x1x2 − 5x2 − x1 + 5 − x1x2 + 5x1 + x2 − 5
=		=
	(x2 − 5)(x1 − 5)

	−4(x2 − x1)
=		< 0 to f↘ (funkcja jest malejąca dla x < 5)
	(x2 − 5)(x1 − 5)

ponieważ: −4 < 0 oraz z założenia x₂ − x₁ > 0 i x₂ − 5 < 0 i x₁ − 5 < 0 Analogicznie określamy monotoniczność dla x > 5

bc: wow ktoś usunoł post, ale dla x>5 funkcja jest niemomotoniczna?

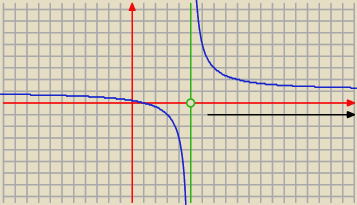
5-latek: To po co sie wygupiasz zamiast sie przylozyc do nauki Nie pisz bzdur ze jest niemonotoniczna Bedzie malejaca Przeciez wykres tej funkcji to hiperbola i asymptota pionowa to x=5

bc: skąd wiesz że głupoty? 5latku zrobiłeś się jakiś nerwowy ale mi wyszło że jest rosnąca i malejąca ,hmm no ćóż no dobra dobra

5-latek: Skad nerwowy tylko akuratnie widzialem ten post caly w kropki