Dowód ograniczenia ciągu zbieżnego w R Skowron: Cześć! Miałem na wykładzie przeprowadzony dowód, że ciąg zbieżny w R jest ograniczony. Wygląda to mniej więcej w ten sposób: |a_n|=|a_n−g+g|≤|a_n−g|+|g| < 1+|g|, gdzie ∊=1, a g to granica ciągu a_n. Do tego momentu rozumiem, ale następuje zapis: M :=max(1+|g|,M₀). Wtedy dla wszystkich n∈N mamy |an|≤ M, gdzie M₀ to element największy w zbiorze. Nie rozumiem, skąd taki zapis M. Jest ktoś, kto byłby w stanie pomóc?

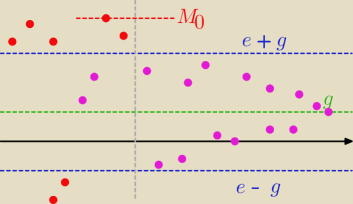
kochanus_niepospolitus: z tamtego szacowania wiesz, że od pewnego elementu wyrazu ciągu spełniają nierówność |a_n| < 1 + |g| , jednak nie musi to być od razu. Jak widzisz na rysunku ... wszystko na prawo od szarej linii mieści się w widełkach (e − g ; e + g) gdzie e=1, ale wcześniej niektóre wyrazy tegoż ciągu 'wyskakiwały' poza te widełki. Wiemy, że takich wyrazów ciągu jest SKOŃCZONA liczba (bo tylko do np. n=10 będą one wyskakiwały), więc możesz jednoznacznie wskazać wśród nich element największy i to będzie Twój M₀

kochanus_niepospolitus: a taki prosty przykład ciągu w którym właśnie wartość największego elementu będzie ograniczeniem:

	10
an =		... jak widzisz tutaj a1 = 10 ; g=0 ... więc pierwszy element nie będzie się
	n

łapał w tych widełkach (zresztą dopiero a₁₁ < 1 = 1 + |g| )

Skowron: kochanus_niepospolitus Dziękuję! Jesteś moim bohaterem!

kochanus_niepospolitus: oj tam od razu bohaterem ... przynajmniej przypomniały mi się pierwsze wykłady z profesorem Gębą z analizy matematycznej ach ten dreszczyk emocji Szkoda, że już po pierwszym kole opadł

Skowron: Nie brzmi to zachęcająco, a analiza i tak nie jest moim ulubieńcem, jak widać zresztą.