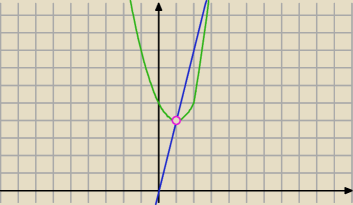
równanie kwadratowe eh: Właśnie powtarzam sobie funkcje kwadratowe I mam taki przykład: x²−4x+2|x−2|+1>0 Chciałbym aby ktoś sprawdził czy mam dobrze: |x−2| = −(x−2), jeżeli x < 2 (x−2), jeżeli x ≥ 2 dla x ≥ 2: x² − 4x +2(x−2) +1 > 0 x² − 2x − 3 > 0 √Δ = 4 x₁ = −1 x₂ = 3 ⇒ x ∊ <2; 3> aby f(x) > 0 dla x ≥ 2 dla x < 2: x² −4x −2(x−2) +1 > 0 x² −6x +5 > 0 √Δ = 4 x₁ = 1 ⇒ x ∊ <1; 2) aby f(x) > 0 dla x < 2 x₂ = 5 dla x=0: 0² −4*0 +2(0 − 2) + 1 > 0 −3 > 0 sprzeczność x ∊ <1; 3>

eh: miała być *nierówność* kwadratowa w opisie, sorki

karty do gry : |x − 2|² + 2|x−2| − 3 > 0 (|x − 2| + 3)(|x − 2| − 1) > 0 |x − 2| > 1 −1< x − 2 < 1 1 < x < 3 Wychodzi na to, że masz dobrze (z dokładnością do nawiasów otwartych)

===: jeden błąd ... zapis przedziału

eh: jak zapisać taki przedział?

karty do gry : albo tak : (1,3) albo tak ]1,3[ bądź tak : 1 < x < 3 Chodzi o to, że przedział ma być obustronnie otwarty.

eh: A faktycznie, zapomniałem o znaku nierówności, dzięki!