Wielomiany
prostezad:
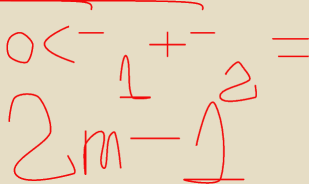
Wielomiany, skąd więło się to 2m−1 przy stosowaniu wzorów Viete'a? Nie mogę tego rozpracować,
co jest tym t1 i t2

Podaję treść zadania: dla jakich m równanie ma pięć pierwiastków?
Zapisując równanie w postaci
x (x
4 + (1− 2m )x
2 + (m
2 − 1)) = 0
widzimy, że równanie ma zawsze pierwiastek x = 0 . Jeżeli podstawimy t = x 2 to pozostaje do
zbadania równanie
t
2 + (1 − 2m )t+ (m
2 − 1) = 0.
Aby równanie miało pięć pierwiastków, powyższe równanie kwadratowe musi mieć dwa
rozwiązania dodatnie (żeby równość 2 t = x dawała cztery różne x −y). Sprawdźmy na początek
kiedy to równanie ma dwa rozwiązania
0 < Δ = (1 − 2m )
2 − 4(m
2 − 1) = 1 − 4m + 4m
2− 4m
2 + 4 = − 4m + 5 4m < 5 ⇒ m < 5/4
Na mocy wzorów Viète’a, rozwiązania będą dodatnie, gdy
0 < t1 + t2 = 2m − 1 ⇒ 1/2< m 0 < t1t2 = m − 1 ⇒ m ∈ (−
∞ ,− 1) ∪ (1,+
∞ ).
Uwzględniając wszystkie warunki mamy m ∈ (1;5/4)
9 paź 13:27
Jerzy:
Ze wzorów Viete'a:
| | − b | | −(1 − 2m) | |
t1 + t2 = |
| = |
| = 2m − 1 |
| | a | | 1 | |
9 paź 13:31
prostezad: Rozumiem, wielkie dzięki za rozpisanie, bo jakoś nie mogłam tego ogarnąć. Jeszcze poprosiłabym
o wytłumaczenie innego zadania:
mx2 − (2m + 1)x + (2 − 3m ) = 0.
Pytanie z treści zadania sprowadza się do pytania kiedy powyższe równanie kwadratowe ma
pierwiastki o dodatniej sumie?
Jezeli równanie jest liniowe, czyli m = 0 , to mamy
−x + 2 = 0 ⇒ x = 2
Jezeli mamy równanie kwadratowe, to sprawdźmy kiedy ma ono pierwiastki
0 ≤ Δ = (2m + 1) − 4m (2 − 3m ) = = 4m2 + 4m + 1 − 8m + 12m2 = 1 6m2 − 4m + 1
Δ = 16− 64 < 0.
Równanie ma więc zawsze dwa pierwiastki. Kiedy ich suma jest dodatnia? – na mocy wzorów Viète’a
ich suma jest równa
0<2m + 1 /m <−−−−−−−−−−−−−−−−− skąd się to wzieło skoro ten wzór stosuje się kiedy delta jest
większa/równa zero, a w poprzedniej linijce wyszło, że jest mniejsza?
9 paź 13:47
Jerzy:
Tam jest policzona "delta z delty"
Δ = 16m2 − 4m + 1
Δ' = (−4)2 − 4*1*16 = 16 − 64 < 0
9 paź 13:51
Jerzy:
No i ... skoro: Δ' < 0 , to wtedy delta "główna" > 0 dla dowolnego m.
9 paź 13:53
5-latek: jewsloi rownanie jest liniowe to nie ma pierwiastkow o dodatniej sumie wiec nie ma potrzeby
rozpatrywanie tego przypadku
9 paź 14:01
prostezad: Już rozumiem, bardzo Wam dziękuję
9 paź 14:10
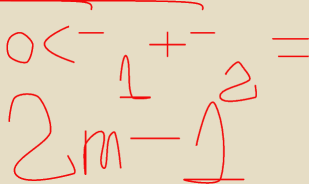 Wielomiany, skąd więło się to 2m−1 przy stosowaniu wzorów Viete'a? Nie mogę tego rozpracować,
co jest tym t1 i t2
Wielomiany, skąd więło się to 2m−1 przy stosowaniu wzorów Viete'a? Nie mogę tego rozpracować,
co jest tym t1 i t2  Podaję treść zadania: dla jakich m równanie ma pięć pierwiastków?
Zapisując równanie w postaci
x (x4 + (1− 2m )x2 + (m2 − 1)) = 0
widzimy, że równanie ma zawsze pierwiastek x = 0 . Jeżeli podstawimy t = x 2 to pozostaje do
zbadania równanie
t2 + (1 − 2m )t+ (m2 − 1) = 0.
Aby równanie miało pięć pierwiastków, powyższe równanie kwadratowe musi mieć dwa
rozwiązania dodatnie (żeby równość 2 t = x dawała cztery różne x −y). Sprawdźmy na początek
kiedy to równanie ma dwa rozwiązania
0 < Δ = (1 − 2m )2 − 4(m2 − 1) = 1 − 4m + 4m2− 4m2 + 4 = − 4m + 5 4m < 5 ⇒ m < 5/4
Na mocy wzorów Viète’a, rozwiązania będą dodatnie, gdy
0 < t1 + t2 = 2m − 1 ⇒ 1/2< m 0 < t1t2 = m − 1 ⇒ m ∈ (− ∞ ,− 1) ∪ (1,+ ∞ ).
Uwzględniając wszystkie warunki mamy m ∈ (1;5/4)
Podaję treść zadania: dla jakich m równanie ma pięć pierwiastków?
Zapisując równanie w postaci
x (x4 + (1− 2m )x2 + (m2 − 1)) = 0
widzimy, że równanie ma zawsze pierwiastek x = 0 . Jeżeli podstawimy t = x 2 to pozostaje do
zbadania równanie
t2 + (1 − 2m )t+ (m2 − 1) = 0.
Aby równanie miało pięć pierwiastków, powyższe równanie kwadratowe musi mieć dwa
rozwiązania dodatnie (żeby równość 2 t = x dawała cztery różne x −y). Sprawdźmy na początek
kiedy to równanie ma dwa rozwiązania
0 < Δ = (1 − 2m )2 − 4(m2 − 1) = 1 − 4m + 4m2− 4m2 + 4 = − 4m + 5 4m < 5 ⇒ m < 5/4
Na mocy wzorów Viète’a, rozwiązania będą dodatnie, gdy
0 < t1 + t2 = 2m − 1 ⇒ 1/2< m 0 < t1t2 = m − 1 ⇒ m ∈ (− ∞ ,− 1) ∪ (1,+ ∞ ).
Uwzględniając wszystkie warunki mamy m ∈ (1;5/4)