sd bc: Jak narysować: https://zapodaj.net/8e719e1324b3b.jpg.html taką funkcję? potrzebuje wskazówek

Omikron: W liczniku zauważ wzór skróconego mnożenia, w mianowniku wyciągnij 2 przed nawias.

5-latek: WItaj Masz juz pomocnika wiec go teraz mecz (dopytuj czego nie rozumiesz

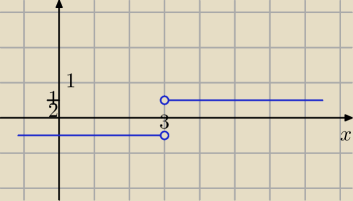
Eta: 1/ √x²−6x+9= |x−3| założenie ; x≠3

	x−3		1
dla x>3 f(x)=		=		−−− f. stała
	2(x−3)		2

	−(x−3)		1
dla x<3 f(x)=		= −		−− f. stała
	2(x−3)		2

bc: wow, czemu √x2−6x+9= |x−3| ? i dlaczego dzielisz na pól ten przedzał? skąd wiesz że w tych 2 przykładach inaczej mogą się zachowywać funkcja

bc: √(x−3)² =| x−3 | wiem

Eta: √a²=|a| to √(x−3)²=|x−3| dla x=3 funkcja nie jest określona dlatego rozpatrujemy przedziały na prawo od trójki czyli dla x>3 wtedy |x−3|= x−3 na lewo od trójki czyli dla x<3 wtedy |x−3|= −x+3= −(x−3) po uproszczeniu otrzymasz to co pisałam wyzej dwie funkcje stałe ........................ jasne? czy jeszcze nie?

bc: ale Df to R−{3} bo tak wynika z mianownika, a ty rozpatrujesz od −oo do 3 i od 3 do +oo dlatego że to wynika z licznika (wartości bezwzględnej?