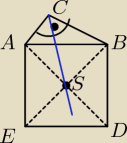
Planimetria. mrr.: Witam Mam pewne zadanie, ktorego nie potrafie zrobic. Na przeciwprostokatnej AB trojkata prostokatnego ABC zbudowano kwadrat ABDE. Udowodnij, ze polprosta CS jest dwusieczna kata ACB, gdzie punkt S jest punktem przeciecia sie przekatnych kwadratu ABDE. Coz zauwazylam, ze AB jest srednica okregu opisanego na tym trojkacie, ale fakt, ze to jest dwusieczna, coz nie potrafie tego udowdnic, po prostu wiem, ze ona nia jest. ;s pomozecie?

mrr.: prosze o pomoc..

mrr.: moze jednak ktos mi pomoze?:(

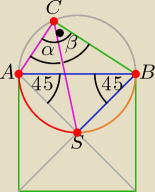
Bogdan: Kąty ABS i ACS to kąty wpisane w okrąg oparte o ten sam łuk AS (czerwony), a więc ich miary są równe sobie, miara kąta ABS wynosi 45^o (kąt między bokiem i przekątną w kwadracie), wobec tego miara kąta ACS też wynosi 45^o. α = 45^o Podobne rozumowanie prowadzimy dla kątów BAS i BCS opartych o łuk SB (pomarańczowy). β = 45^o α = β Stąd półprosta wychodząca z punktu C i przechodząca przez punkt S jest dwusieczną kąta ACB.