logarytmy - zadania Kasia:

	log2x4
a) logx28+logx48<
	log2x2−4

b) log_x2*log_2x2*log₂4x>1 Proszę o pomoc, nie wiem jak się za to zabrać

iteRacja: a/ założenia zrób jak zawsze na początek lewa strona skorzystaj z tw. a=/= 1, a>0, b>0

	1
loga b =
	logb a

będziesz mieć log o tych samych podstawach

Jerzy: W zadaniach pozamieniaj na logarytmy o podstawie 2 i podstaw: log₂x = t

Kasia: Dziękuję za odpowiedzi, ale nie chce mi to niestety wyjść, może ktoś chociaż jeden mi pokaże?

Jerzy: Np:

	log28		3		3
logx/28 =		=		=
	log2(x/2)		log2x − log22		t − 1

Jerzy: log₂x⁴ = 4log₂x = 4t

Jerzy:

	3
logx/4 =
	t − 2

'Leszek: a) jest w podreczniku gotowy wzor na zamiane postawy logarytmu !

	loga c
log b c =
	log a b

	log 2 8
Czyli jak proponuje Jerzy : log x/2 8 =		=
	log 2 (x/2)

	3
=
	log2 − 1

Eta: b) D: x>0 i x≠1 i 2x≠1 ⇒ x∊(0,∞)\ {1/2, 1}

1		1
	*		*(2+log2x)>1 log2x=t
log2x		1+log2x

2+t
	>1
t(1+t)

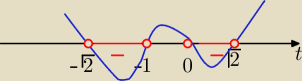
[2+t−t(1+t)]*t(1+t)>0 (−t²+2)*t(t+1)>0 (t+√2)(t−√2)*t*(t+1)<0 log₂x∊(−√2,−1) lub log₂x∊(0,√2) ........................ Odp: x ∊(2^−√2, 1/2) U ( 1, 2^√2) ======================