| 1 | 2 | ||
+ | <1 | ||
| 5−logx | logx+1 |
| 1 | 1 | |||
x∊(0, | ) suma ( | ,100000) suma (100000,∞) | ||
| 10 | 10 |
| 1 | 1 | ||
<1+ | |||
| log2x | log2x−1 |

 1/ założenia; dobrze
można napisać ładniej : x∊(0,∞)\{1/10, 105}
logx=t
[t+1+10−2t−1(5−t)(t+1)]*(5−t)(t+1)<0
(t2−5t+6)(t−5)(t+1)>0
(t−3)(t−2)(t−5)(t+1)>0
......
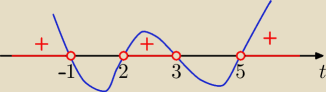
logx<−1 lub (logx>2 i logx<3) lub logx>5
x<1/10 lub x ∊(100, 1000) lub x∊(100 000, ∞) i x>0
Odp: x∊(0,1/10) U(100,1000) U (100 000,∞)
===============================
2/ podobnie...
1/ założenia; dobrze
można napisać ładniej : x∊(0,∞)\{1/10, 105}
logx=t
[t+1+10−2t−1(5−t)(t+1)]*(5−t)(t+1)<0
(t2−5t+6)(t−5)(t+1)>0
(t−3)(t−2)(t−5)(t+1)>0
......
logx<−1 lub (logx>2 i logx<3) lub logx>5
x<1/10 lub x ∊(100, 1000) lub x∊(100 000, ∞) i x>0
Odp: x∊(0,1/10) U(100,1000) U (100 000,∞)
===============================
2/ podobnie...
 Dziedzina dobrze.
logx=t
Dziedzina dobrze.
logx=t
| 1 | 2 | ||
+ | −1<0 | ||
| 5−t | t+1 |
| t+1+2*(5−t)−(5−t)*(t+1) | |
<0 | |
| (5−t)*(t+1) |
| t+1+10−2t−(5t+5−t2−t) | |
<0 | |
| (5−t)*(t+1) |
| t2−5t+6 | |
<0⇔ | |
| (5−t)*(t+1) |
| (t−2)*(t−3) | |
<0⇔ | |
| (5−t)*(t+1) |
| 1 | ||
x∊(0, | lub x∊(100,1000) lub x∊(100 000,∞) | |
| 10 |
 Udało mi się zrobić drugi:
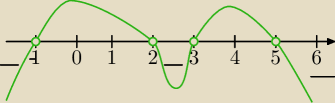
D=(0,1) suma (1,2) suma (2,∞)
Udało mi się zrobić drugi:
D=(0,1) suma (1,2) suma (2,∞)
| 1 | 1 | ||
−1− | <0 | ||
| t | t−1 |
