 Zadanie
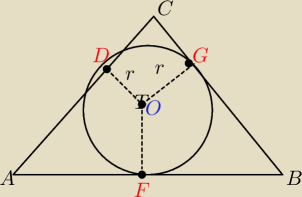
Wykaz ze jesli w trojkacie prostokatnym r i R sa odpowiednio promieniami okregu wpisanego i
opisanego to obwod L= 2r+4R
AB= 2R
DC=r i CG=r
AC+CB= AD+CD+CG+GB
AC+CB= AD+GB+2r
ale
AD=AF i GB= FB
AC+CB= AF+FB+2r
ale AF+FB= AB= 2R
AC+CB= 2R+2r
L= AC+CB+AB= 2R+2r+2R= 4R+2r
Ale Eta z polem muszse pomyslec
ma byc S= r2+2rR
Zadanie
Wykaz ze jesli w trojkacie prostokatnym r i R sa odpowiednio promieniami okregu wpisanego i
opisanego to obwod L= 2r+4R
AB= 2R
DC=r i CG=r
AC+CB= AD+CD+CG+GB
AC+CB= AD+GB+2r
ale
AD=AF i GB= FB
AC+CB= AF+FB+2r
ale AF+FB= AB= 2R
AC+CB= 2R+2r
L= AC+CB+AB= 2R+2r+2R= 4R+2r
Ale Eta z polem muszse pomyslec
ma byc S= r2+2rR
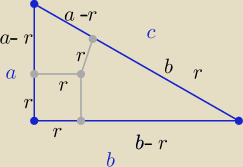 Obwód
prościej: ( wprowadzaj oznaczenia małymi literkami)
a−r+b−r=c i c=2R ⇒ a+b=2r+c⇒ a+b=2r+2R
L=a+b+c=2r+4R
c.n,w
Obwód
prościej: ( wprowadzaj oznaczenia małymi literkami)
a−r+b−r=c i c=2R ⇒ a+b=2r+c⇒ a+b=2r+2R
L=a+b+c=2r+4R
c.n,w

| a−r+r)(b−r+r) | ||
P= | ||
| 2 |
| a*b | ||
P= | ||
| 2 |
| ab | ||
P= | i P=(a−r)(b−r) | |
| 2 |
| ab | ab | ||
=ab−ar−br+r2 ⇒ | =r(a+b)−r2 i a+b=2r+2R | ||
| 2 | 2 |
| ab | |
=P=r2+2rR | |
| 2 |
 Sam niestety nie doszedlbym do tego .
Sam niestety nie doszedlbym do tego .