zbiór wartości i dziedzina tangjinjaem: Wyznacz dziedzinę i zbiór wartości funkcji:

	1
a) f(x) =
	1 − tg2x

dziedzina mi wyszła tak:

	π		π		π		kπ
x ≠		+kπ V x ≠ −		+kπ => x ≠		+
	4		4		4		2

	π		kπ
czyli D = R \ {		+		}
	4		2

a zbioru wartości nie potrafię wyznaczyć : /

Adamm: po pierwsze, dziedzina tangesa czyli x≠π/2+kπ, k∊ℤ po drugie tg²x≠1 ⇔ tgx≠1 ∧ tgx≠−1 ⇔ x≠π/4+kπ/2 D=ℛ\(∪_k∊ℤ{π/4+kπ/4}) inna sprawa t=tg²x∊<0; ∞) i mamy zbiór wartości funkcji

	1
f*(t)=		dla t∊<0; ∞)
	1−t

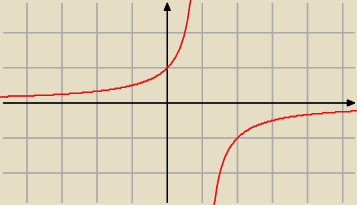
rysujemy hiperbolę f należy do (−∞; 0)∪<1; ∞) no i mamy zbiór wartości

tangjinjaem: dziękuję

tangjinjaem: Tylko mam takie pytanie, bo jak narysuję sobie wykres tej funkcji f(x) = 1/(1−tg²x) w programie to zbiór wartości wychodzi (−∞;0> ∪ <1;∞) czyli jest domknięty przy 0, to czemu tu tak nie wyszło?

iteRacja: dziwny ten wynik (−∞;0> ∪ <1;∞) 0 należy do zbioru wartości funkcji tylko wtedy, gdy funkcja ma miejsca zerowe a f(x) = 1/(1−tg²x) jak widać, nie ma miejsc zerowych

tangjinjaem: w sumie racja, nie wiem czemu tak wyszło na wykresie