funkcja odwrotna michał: Cześć mam do was pytanko mam zrobić odwrotność funkcji y=x²−2x. x∊<1,+∞) i wykres wyglada tak : x=1+sqrt{1+y} czy da się zamienić algebraicznie wzór y=x²−2x na f⁻¹

michał: już ogarnąłem że muszę uzyc wzoru skroconego mnożenia

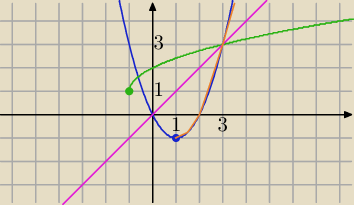
Mila: y=x²−2x X_w=1 funkcja jest różnowartościowa dla x≥1, y=(x−1)²−1 y+1=(x−1)² x−1=√y+1 x=√y+1+1 zamiana zmiennych y=√x+1+1 wykresy symetryczne względem prostej y=x

michał: Podbijam Mila może pomożesz mi z narysowaniem wykresu y=cos(arccosx) Nie mam pojecia jak to zrobić

Adamm: najpierw: dziedzina x∊<−1; 1> dalej y=x (cosx to funkcja odwrotna do arccosx) no i rysujesz, to funkcja liniowa

michał: Adamm mógłbyś wytłumaczyć mi to bardziej szczegółowo ?

Adamm: słuchaj, mogę gadać bzdury o tym samym ale fajniej byłoby gdybyś to TY wytłumaczył czego nie rozumiesz

michał: wiem że arccos to odrwrotność cosx,ale ,nie mam pojęcia w jaki sposób wykres to f.limiowa

Adamm: z definicji funkcji odwrotnej mamy f(f⁻¹(x))=x oraz f⁻¹(f(x))=x to jest po prostu własność funkcji odwrotnej

michał: noo taak Dziękuje Ci Adamm a cały czas miałem przed sobą książkę i tego nie widziałem Tak jeszcze zapuytam,w przypadku funkcji y=arccos(cosx)dlaczego wychodzi taki zygzak ?

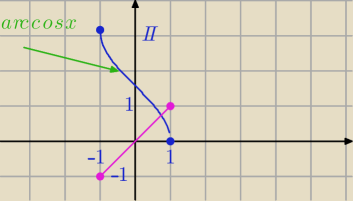
Mila: wykres y=cos(arccos(x)) y=x

Adamm: patrz tym razem dziedzina = ℛ to prawda że te funkcję są do siebie odwrotne, ale bierzemy przy tym przedział dla cosinusa x∊[0; π] czyli dla x∊[0; π], to faktycznie, y=x potem od x∊[π; 2π] mamy zaczynając od punktu w którym skończyliśmy, y=−x+2π no bo wykres cosinusa jest symetryczny dla tego przedziału no i jak sobie narysujesz to już w przedziale, to popatrz że ta funkcje jest okresowa o okresie 2π więc wystarczy to co sobie narysowałeś "przekalkować", i wychodzi taki zygzak

michał: zastanawiam się jeszcze dlaczego dzidziną są liczby rzeczywiste..

Adamm: no, cosx to masz dziedzina ℛ arccosx to masz dziedzina [−1; 1], ale cosx∊[−1; 1] więc dziedzina to ℛ i jeszcze z tym, łatwiej byłoby uzasadnić dla x∊[−π; 0] masz arccos(cosx)=arccos(cos(−x))=−x (no bo −x∊[0; π]) i łatwiej sobie chyba narysować y=−x dla x∊[−π; 0] i x dla x∊[0; π], i dopiero teraz przekalkować

michał: ok już wszytsko rozumiem,Adamm bardzo Ci dziękuje odwaliłeś kawał dobrej roboty

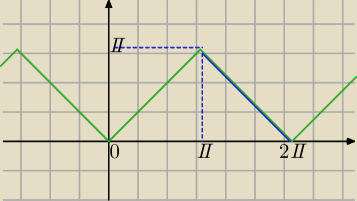
Mila: 2) Wykres: y=arccos(cosx) y=x dla x∊<0,π> dla x∊(π,2π> musimy przekształcić x=π+u, gdzie u∊(0,π> cos(π+u)=−cos(u) y=arccos(cos(π+u))=arccos(−cos(u))=π−arccos(cos(u))=π−u⇔ y=π−u=π−(x−π) y=−x+2π

Adamm: Mila, wystarczyło cosx zapisać tak, by jego argument należał do przedziału (π; 2π> czyli cosx=cos(2π−x) 2π−x∊<0; π) prościej? moim zdaniem tak i bez używania tych wszystkich gotowych wzorów

Adamm: miałem na myśli, by należał do przedziału <0; π>, oczywiście

Mila: Można.