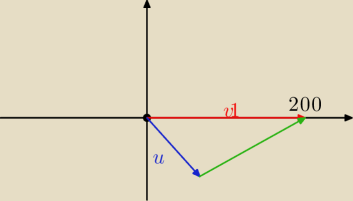
Pilot samolotu chce osiągnąć punkt 200 km na wschód od obecnego położenia. Wiatr
wieje z prędkością 30 km/h z północnego zachodu. Obliczyć wektor jego prędkości w
stosunku do poruszającej się masy powietrza, jeżeli według rozkładu lotu miał przybyć do
miejsca przeznaczenia po 40 min.
v1 = v = 300km/h
u = 30km/h
Położenie pilota początkowe (0,0)
Cel pilota (200,0)
Niebieska strzałka obrazuje, jaką drogę przebędzie pilot przez wiatr, czyli 20km, czerwona cel
pilota
20 = a√2
a=10√2
Położenie pilota uwzględniając wiatr (10√2, −10√2)
Wektor drogi (200−10√2, 10√2)
**** Teraz czarna magia, nie wiem czy dobrze to robię, na logikę próbowałem
Vx = Sx/t
Vy=Sv/t
| 200−10√2 | ||
Vx = | = 300 − 15√2 | |
| 2/3 |
| 10√2 | ||
Vy = | = 15√2 | |
| 2/3 |
