s garnek: Oblicz prędkość liniową i przyspieszenie dośrodkowe punktów powierzchni kuli ziemskiej leżących na równiku i szerokości geograficznej 60 stopni. Promień Ziemi przyjmij jako 6400 km.

'Leszek: Dla rownika :

	2πR		2π 6400000 m
v=		=		= ....... predkosc liniowa (m/s)
	T		24 *3600 s

	v2
a=		= ........., przyspieszenie dosrodkowe ( m/s2 )
	R

Dla szerokosci geograficznej φ = 60° r = R * cos φ = 6400000* 0,5 = 3200000 m

	2πr		2π 3200000 m
v =		=		= .............(m/s)
	T		24* 3600 s

	v2
a=		= .........(m/s2 )
	r

garnek: Skąd wziął się cos z szerokości? Nie rozumiem tego kroku Mogę prosić o wyjaśnienie? Mam rysunek, ale niezbyt do mnie przemawia...

'Leszek: r − odleglosc danego punktu na szerokosci φ od osi obrotu Ziemi , Z rysunku : r = R* cos φ

garnek: Dlaczego akurat razy cos?

'Leszek: Trygonometria ! ! !

Janek191:

r
	= cos φ
R

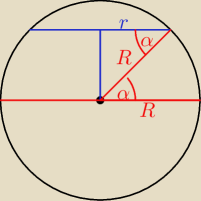
Janek191: α = 60^o

zupaa: Rozumiem, DZIEKUJE