Jak wyliczyć długość dwusiecznej kąta (w trójkącie NIEprostokątnym) ? zgredek: Długości boków AC i BC trójkąta ABC są odpowiednio równe 5 cm i 8 cm. Kąt między tymi bokami ma 60 stopni. Oblicz długość dwusiecznej kąta ACB i długość boku AB. Z tego co wyliczyłem AB = 7, ale skąd mam wyliczyć długość dwusiecznej ACB?

iteRacja: skorzystaj z tw. cosinusów, dotyczy dowolnego trójkąta

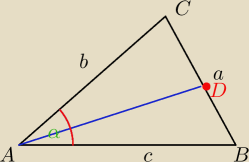
5-latek: Ogolnie Jeski kąt miedzy bokami AC i AB oznaczymy α to dlugosc odcinka dwusiecznej AD kata A jest rowna

	2bc		α
AD=		*cos
	b+c		2

Pozostale odcinki dwusieczych inych katow otrzymujesz przez cykliczne przestawienie a, b c Zastosuj to do swojego zadania

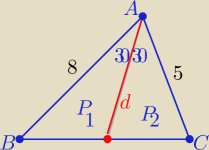
Eta: P(ABC)=0,5*8*5sin60^o= 10√3

	5
P1=4*d*sin30o= 2d , P2=0,5*5*d*sin30o=		d
	4

P(ABC)=P₁+P₂

13
	d=10√3 ⇒ d=.................
4

zgredek: Wielkie dzięki!

Eta: Widzę,że błędnie oznaczyłam trójkąt Popraw oznaczenia na moim rysunku ( zgodnie z treścią Obliczenia są ok