obód trójkata kamam: W trójkącie równoramiennym ABC ( AB=AC), punt M lezy na BC tak ze BM=CM .∡BXC=3∡BAC gdzie X jest punktem na AM. Oblicz obwód trójkata ABC jesli AX=10,AM=11.

5-latek: Terzz troche pomysl sam

Adamm:

	x
tgα=
	11

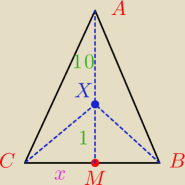
tg(3α)=x 0<3α<π 0<α<π/3 ⇒ 0<x

	3(x/11)−(x/11)3
tg(3α)=
	1−3(x/11)2

	363x−x3
x=
	1331−33x2

1331−33x²=363−x² 32x²=968

	121
x2=
	4

	11
x=
	2

	11
AC=√121/4+121=		*√5
	2

obwód = 11√5+11

Adamm: skorzystałem ze wzoru

	3tgα−tg3α
tg(3α)=
	1−3tg2α

Adamm: w sumie to nie wiem czemu pisałem 0<α<π/3 ⇒ 0<x skoro x>0 tak czy siak jedyne co z tego wynika to że x<11√3

kasia: kamam, podaj odpowiedź, jeśli masz.

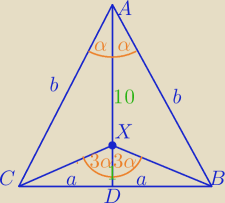
Mila: 1) W ΔADB

	a
tgα=		⇔a=11tgα, tgα>0
	11

2) W ΔXDB:

	a
tg(3α)=		=a
	1

3) a=11tgα i a=tg(3α)⇔ 11tgα=tg(3α)⇔

	3−tg2α		3−tg2α
11tgα=tgα*		⇔ 11=
	1−3tg2α		1−3tg2α

11−33tg²α=3−tg²α 32tg²α=8

	1		1
tg2α=		i tgα>0 ⇔tgα=
	4		2

4)

a		1		11
	=		⇔a=
11		2		2

|AB|=11

	605
b2=5.52+112=30.25+121=151.25=
	4

	√121*5		11√5
b=		=
	2		2

5) Ob=11*(√5+1)