proszę o rozwiązanie Anna: zbadaj równowartościowość funkcji f(x) = 3x² −1 dla x ∊R oraz g(x)= 2x +4 dla x ∊ <−4; 2> f(x₁) =f(x₂) ⇒ x₁ = x₂ 3x₁² −1 =3x₂² −1 ⇒ x₁ =x₂ g(x₁)=g(x₂) ⇒ x₁ = x₂ 2x₁+4 = 2x₂ +4 ⇒ x₁ =x₂ dla x ∊ <−4;2> ale co z przedziałem

Jerzy: A co to jest funkcja równowartościowa ?

5-latek: Dwie funkcje liczbowe jednej zmiennej sa rownowartosciowe jesli ich obszary okreslonosci (dziedziny sa identyczne oraz wartosci obu funkcji sa sa rowne dla kazdej liczby z dziedziny

Jerzy: Gdzie znalazłeś taką definicję ?

Anna: przepraszam ma tam być napisane różnowartościowość a nie równowartościowość

Jerzy: No właśnie Znasz definicję takiej funkcji ?

5-latek: Jerzy Jan Lesniak O funkcjach jednej zmiennej BM nr 14 (1963r)

Jerzy: Przyznam Ci sie szczerze,że nigdy nie spotakałem się z takim pojęciem

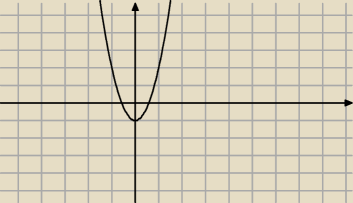
5-latek: Dla pierwszej funkcji y=3x²−1 podajemy kontrprzyklad dla x=−1 f(x)= 2 i x=1 f(x)=2 funkcja nie jest roznowartoscowa Dla drugiej sama

Jerzy: Funkcja jest różnowartościowe jeżeli: ⋀ x₁,x₂ ∊ D : x₁ ≠ x₂ jest: f(x₁) ≠ f(x₂) ⇔ f(x₁) − f(x₂) ≠ 0 f(x₁) − f(x₂) = 3x₁² −1 − 3_x(2² +1 = 3(x₁ + x₂)(x₁ − x₂) Widać,że dla: x₁ = − x₂ f(_x1) = f(x₂) , a więc nie jest róznowartościowa .

5-latek: Tylko zauwaz ze tam sa porownane dwie funkcje Nie ma jednej funkcji rownowartosciowej

Jerzy: 2) f(x₁) − f(x₂) = 2x₁ + 4 − 2x₂ − 4 = 2(x₁ − x₂) ≠ 0 dla dowolych róxnych x₁ , x₂ czyli funkcja jest różnowartościowa

Jerzy: W zadaniu jest mowa o różnowartościowości.

Jerzy: I nie widzę w treści żadnego porównania , natomiast widzę słowo "zbadaj"

5-latek: Tak pozniej poprawila jesli natomiast nie porawilaby to te funkcje f(x) i g(x) nie sa rownowartosciowe bo ich dziedziny nie sa rowne .

5-latek: natomiast jesli chodzi o roznowartosciowsc to kiedys Godzio mi odpisal ze jesli podamy kontrprzyklad na to ze dla dwoch argumentow wartosci funkcji sa rowne to nie musimy badac z defincji roznowartosciowosci

Anna: dziękuję

Jerzy: małolat .. z całym szacunkiem dla Godzia , nie jest on dla mnie wyrocznią. Co wiecej w poleceniu zadania masz słowo zbadaj , a nie wykaż ( pokaż ) , co stanowi dużą różnicę. Dla wykazania różnowartościowośći funkcji liniowej, ciężko jest podać kontrprzykład.

Blee: 5−latek zadanie nie polegalo na porownaniu dwoch funkcji tylko to byly dwa osobne podpunkty. Natomiast prawda jest ze wystarczy podac jeden przyklad dla ktorego (w zadanym przedziale) funkcja nie jest roznowartosciowa aby mozliwe bylo napisanie ze ona nie jest (w zadanym przedziale), jednak do tego potrzebna jest wiedza o tym jak (pi razy oko) wyglada wykres funkcji a tej wiedzy autorka nie posiada. Autorka bedzie takie zadania robila 'jak automat' wiec bedzie robila to z definicji

5-latek: Ze slowem zbadaj , wykaz, pokaz jest tak samo jak ze slowem uzasadnij udowodnij . Kiedys uzasdnilem slownie ze y=x*|x| jest roznowatosciowa to Kacper (nauczyciel) napisal ze mam to udowodnic . W ksiazce Anusiak do klasy 1 tak samo napisal o kontrprzykladzie . Tak samo Gewert Skoczylas . Poza tym Anna powinna znac wykres funkcji kwadratowej i wiedziec ze nie jest ona rosnaca albo malejaca w calej swojej naturalnej dziedzinie tak samo powinna znac wykresy innych funkcji jednej zmiennej z liceum bo to jest studentka . Co do funkcji liniowej to nie zartuj sobie

5-latek: Dzien dobry Ajtek

Jerzy: Może "krakowskim targiem" ..... jeśli w treści zadania jest "zbadaj na podstawie definicji różnowartościowość funkcj " , to robimy tak jak pokazałem, w innym przypadku dopuszczmy kontrprzykład

5-latek: Dobrze Krakowianinie

Jerzy: