Zbiory Hiro: Zbiory Ile liczb postaci 1/2k gdzie k jest liczbą całkowitą należy do zbioru A∩B? b) A=(−2;∞), B=<−1;1)U(2;3) c) A=(−1;0>, B=<−2;2)U(3;5) d) A=<1;6>, B=(2;3>U<4;5>

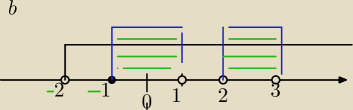
5-latek: w b ) jedna Pozostale przypadki podobnie

Hiro: Z odpowiedzi wynika, że: b) 5 c) 2 d) 5 Problem w tym, że nie wiem jak to rozwiązać...

iteRacja: 5−latku witaj ponownie w dniu dzisiejszym!

	1		1
Hiro, czy chodzi w treści jest		, czy może		*k (wtedy jest pięć rozwiązań)
	2k		2

5-latek: Dobry wieczor Juz myslalem ze sie pogniewalas na mnie .

Hiro: W treści jest ¹₂k

5-latek: ja to zadanie zrozumialem tak do zbioru A∩B naleza dwie liczby calkowite K k=−1 ik=0 Przez o dzielic nie wolno wiec zostaje

1		1		1
	=		= −
2k		2−1		2

	1
nawet jesliby likczba byla postaci		k to wtedy dwie liczby ale moze nie tak zrozumialem
	2

iteRacja : Panowie czyli ostatecznie ustalamy

	1
Ile liczb postaci		*k należy do zbioru A∩B, jeśli k jest liczbą całkowitą ?
	2

dlaczego tak? bo wtedy nasze rozwiązanie zgodzi się z tym z podręcznika

Hiro: Tak, a mogłabyś wytłumaczyć jak to rozwiązać?

5-latek: To proszse napisz jakie beda wtedy te liczby bo ja tego nie rozumiem

iteRacja : A∩B = <−1;1)U(2;3)

	−1		−1		0		1		5
do tego przedziału należą liczby		=−1,		,		=0,		,
	1		2		2		2		2

jest ich pięć

iteRacja : liczby podałam właściwe ale postać muszę poprawić

1
	*(−2) = −1
2

1		−1
	*(−1) =
2		2

1
	*0 = 0
2

1		1
	*1 =
2		2

1		5
	*5 =
2		2

iteRacja : czy się ze mną zgodzicie?

5-latek: czyli ta liczba postaci U[1}{2}k ma nalezec do wspolnej czesci zbioru a nie liczba calkowita k Wtedy sie zgadzam

Hiro: Czyli analogicznie w przykładzie c to liczby −1 i 0, a w przykładzie d 2¹₂, 3, 4, 4¹₂ i 5?

iteRacja : dwa razy tak ⇔ 5−latek − tak ∧ Hiro − tak

Hiro: Dzięki

5-latek: Dzieki i pozdrawiam

Hiro: Dzięki

iteRacja : praca zespołowa jest najlepsza