proszę o sprawdzenie Anna:

	x2 −6x +9
dana jest funkcja o wzorze f(x) =
	ax −3

a) określ dziedzinę i narysuj wykres funkcji dla a =1 b) wyznacz a tak aby do wykresu funkcji należał punkt a=(2; −1) c) wyznacz a tak aby dziedziną funkcji był zbiór R−{5} ja rozwiązałam tak a) Df =R

	x2 −6x +9		(x−3)2
f(x) =		=
	x −3		x−3

wykresem jest prosta y= x − 3

	16
b) −1=		⇒ a = 13
	−a −3

c) a= 15 proszę o sprawdzenie

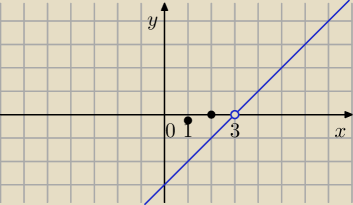
Janek191: Dla a = 1 Df = ℛ \ {3} Wykresem jest prosta bez jednego punktu

Janek191:

	4 − 12 + 9
b) − 1 =
	2 a − 3

	1
− 1 =
	2a − 3

2a − 3 = − 1 2 a = 2 a = 1 =====

Janek191:

	3
c) a =
	5

Anna:

	3
jak obliczyłeś że a =
	5

Anna: dziękuję

Janek191: 5a − 3 = 0 5a = 3

	3
a =
	5

===========

Anna: jeszcze raz dziękuję

Janek191: