Rozwiąż równanie groklin: 3x³−8x²−15x−4≥0 Pomoże ktoś, bo w żaden sposób mi nie wychodzi?

Eta: W(−1)=−3−8+15−4=0 x=−1 jest pierwiastkiem W(4)=3*64−8*16−15*4−4=..=0 x= 4 jest pierwiastkiem wykonaj dzielenie przez (x+1)(x−4) otrzymasz (3x+1)(x+1)(x−4)≥0 x= −1/3 −− jest pierwiastkiem Odp: x∊<−1,−1/3> U <4,∞)

yht: W(x) = 3x³−8x²−15x−4 W(−1) = 0 W(x) jest podzielny przez (x+1) W(x) : (x+1) = P(x) P(x) = ax²+bx+c W(x) = (ax²+bx+c)(x+1) W(x) = ax³+ax²+bx²+bx+cx+c W(x) = ax³+(a+b)x²+(b+c)x+c W(x) = 3x³−8x²−15x−4 a=3, (a+b)=−8, (b+c)=−15, c=−4 a=3, b=−11, c=−4 P(x) = 2x²−11x−4 Δ=(−11)²−4*2*(−4) = 121+32 = 153 √Δ = 3√17

	11−3√17
x1=
	4

	11+3√17
x2=
	4

Eta: (3x+1)(x+1)(x−4)= 3x³−8x²−15x−4

yht: poprawka 5−tej linijki od końca: P(x) = 3x²−11x−4 Δ = 169 → √Δ = 13

	11−13		1
x1 =		= −
	6		3

	11+13
x2 =		= 4
	6

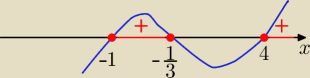
wykres i ... odp. x ∊ <−1,−1/3> ∪ <4, +∞)

Eta: