pochodna Ola: W kulę o średnicy d wpisujemy walce. Przedstaw pole powierzchni tych walców jako funkcję ich wysokości. Zbadaj przebieg zmienności tej funkcji i naszkicuj jej wykres.

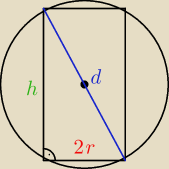
yht: h² + (2r)² = d² 4r² = d²−h²

	d2−h2
r2 =
	4

	√d2−h2
r =
	2

P = 2π*r² + 2π*r*h

	d2−h2		√d2−h2
P(h) = 2π*		+2π*		* h
	4		2

	d2−h2
P(h) = π*		+h*√d2−h2
	2

	(−2h)
P'(h) = −π*h + h*		+√d2−h2
	2√d2−h2

	h2
P'(h) = −π*h−		+√d2−h2
	√d2−h2

	h2
P'(h)=0 ⇔ −π*h−		+√d2−h2 = 0 |*√d2−h2
	√d2−h2

−π*h*√d²−h² − h² + d²−h² = 0 d²−2h² = h*√d²−h² |:h

d2
	− 2h = √d2−h2 |()2
h

d4
	− 4d2 + 4h2 = d2−h2
h2

d⁴ − 4d²*h² + 4h⁴ = d²*h² − h⁴ 5h⁴−5d²*h²+d⁴ = 0 h² = x 5x²−5d²*x + d⁴ = 0 Δ = (−5d²)²−4*5*d⁴ = 25d⁴−20d⁴ = 5d⁴ √Δ = √5d² x₁ = ... x₂ = ... h₁ = ... h₂ = ...