funkcja liniowa 00000: Wyznacz wartości parametru m, dla których równanie x−|4−2x|=2m ma dwa rozwiązania a) dodatnie b) przeciwnych znaków. Czy mógłby mi ktoś wytłumaczyć jak w ogóle zabrać się za takie zadanie, bo nie mam żadnej koncepcji?

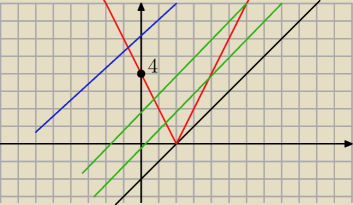
5-latek: Przeksztalcic to rownanie do postaci −|4−2x|= −x+2m |4−2x|= x−2m na rysowac w ukladzie wspolrzednych wykres funkcji y= |4−2x|i y=x−2 i zobaczyc jakie bedzie m Zauwaz ze po osi OY od (−2do 4) masz dwa rozwiazania dodatnie od (4,∞) dwa rozwiazania przeciwnych znakow wiec wyznacz to m

00000: dlaczego muszę narysować y=x−2 skoro tam jest x−2m?

5-latek: Po to zeby byl punkt odniesienia Zauwaz ze dla m=1 mmasz y= x−2 i masz tylko jedno rozwiazanie Teraz wez np m=2 wobec tego y=x−2m= x−4 prosta y=x−4 nie ma w ogole punkow wspolnych z y= |4−2x| Wiec juz widzimy z eby byly dwa rozwiazania dodatnie to m musi byc <1 ale tez >−2 bo dla m=−2 masz y=x−2m to y=x−2*(−2)= x+4 Narysuj sobie wykres y=x+4 to zobaczysz ze nie bedzie dwox ch rozwiazan dodatnich tylko jedna x=0 i drucie x>0 czyli naszse m∊(−2,1) Wiec narysuj sobie kilka wykresow dla m z tego przedzialu y=x−2m i podstzwiaj m Teraz znaki przeciwnw to widzisz ze wykres funkcji y=x−2m musi lezec powyzej punktu (0,4) wiec m ∊(−∞,−2)

00000: Dziękuję!