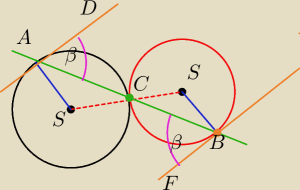
Okregi -kąty 5-latek: Przez punkt stycznosci dwoch okregow prowadzimy prosta przecinajaca jeden z nich w punkcie A a drugi w punkcie B Udowodnij ze styczne do tych okregow poprowadzone w punktach A i B sa rownolegle W poprzednim zadaniu wykazalismy ze katy srodkowe oparte na lukach lezacych po przeciwnych stronach wyznaczonych przez taka prosta sa rowne Wobec tego korzystajac z twierdzenia o kacie miedzy styczna a cieciwa (kat ten jest rowny polowie kąta srodkowego Stweirdzamy ze kąt DAC jest rowny kątowi CBF Z tego wynika ze te stczne AD i FB sa rownolegle

5-latek:

iteRacja: Witaj! Proponuję sposób bez twierdzenia o kątach środkowych, o którym piszesz. przez S₁ oznaczam środek pomarańczowego okręgu <ACS = <S₁CB (kąty wierzchołkowe mają równe miary) ΔACS równoramienny AS=SC (promienie) ⇒ <ACS = <SAC ΔS₁CB równoramienny CS₁=SB (promienie) ⇒ <S₁CB =<S₁BC a więc <SAC = <S₁BC <CAD= 90^o − <SAC <CBF= 90^o − <S₁BC <CBF=<CAD AD∥FB

5-latek: dziekuje Ci