Jak zbadać czy ciągi są monotoniczne od pewnego miejsca. Beneliu: Jak zbadać czy ciągi są monotoniczne od pewnego miejsca. Umiem badać monotoniczność ciągów przez odjęcie a_n+1−a_n ale tu doszło aby badać od pewnego miejsca. za skarby nie wiem o co chodzi. mógłby ktoś wytłumaczyć na tym przykładzie?

	n2+1
an=
	n!

Blee:

an+1
an

Jezeli iloraz wiekszy id 1 to rosnacy, jezeli mniejszy od 1 to malejacy jest ciag

Beneliu: tylko co oznacza "od pewnego miesjca"

Mila:

	(n+1)2+1
an+1=
	(n+1)!

	n2+2n+2
an+1=
	n!*(n+1)

	n2+2n+2		n2+1
an+1−an=		−		=
	n!*(n+1)		n!

	1		n2+2n+2		n2+1
=		*(		−		)=
	n!		(n+1)		1

	1		−n3+n+1
=		*
	n!		n+1

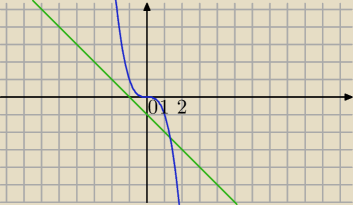
Badasz znak tej różnicy, wystarczy zbadać znak licznika Przypuszczam, że od pewnego n ciąg jest malejący −n³+n+1<0⇔ −n³<−n−1 Dla n≥2 wykres y=−n³ leży pod wykresem g(n)=−n−1⇔ ciąg a_n malejący dla n≥2

Beneliu: A na jakiej podstawiue przypuscilas że od pewnego miejsca ciag Jest malejacy

Jerzy: Popatrz na wykres to zobaczysz, że od pewnego n wykres niebieski ( −n³) leży poniżej wykresu zielonego (−n − 1) , a to oznacza, że: −n³ + n + 1 jest ujemne.

Beneliu: To dla n<2 ten ciag jest rosnący? Czy niemalejący?

iteRacja: n<2 dla mamy ytlko jeden wyraz ciągu a₁ wyraz pierwszy bo tylko 1<2 pytanie czy ciąg maleje czy rośnie nie ma sensu przy jednym razie a₁, bo nie ma z czym porownac

Jerzy: Patrz komentarz wyżej.

Beneliu: Ale gdyby bylo wiecej wyrazów. Zalozmy wyrazy zaczynały by sie od n=−5

Jerzy: A potrafisz bez obliczania ustalic , od którego wyrazu ciąg: a_n = (n − 6)(n − 10) jest rosnący ?

Jerzy: n jest liczbą naturalną, więc zapis: n = −5 jest bez sensu

Beneliu: Od wierzchołka? 8?

Jerzy: Dokładnie tak.

Beneliu: Ale a_n=(n−6)(n−10) Dla n<8 jest majejacy? Bo funkcja wtedy maleje

Jerzy: Tak, dla n < 8 jest malejący.