Funkcja homograficzna Jacek:

	x
Uzasadnij, że dla każdej liczby rzeczywistej m równanie		= m ma przynajmniej
	|x|−2

jednorozwiązanie Pomoże ktoś ? Ja rozwiązałbym to graficznie, ale niestety nie umiem narysować tej funkcji Z góry dzięki za pomoc

karty do gry :

	x
f(x) =
	|x| − 2

lim_{x → −2⁺} = ∞ lim_{x → 2⁻} = −∞ Koniec.

Jacek: Sorki, ale nic z tego nie rozumiem Nie miałem jeszcze granic

karty do gry : To rozpisuj dla x ≥ 0 i x≠ 2 oraz dla x < 0 i ≠ − 2

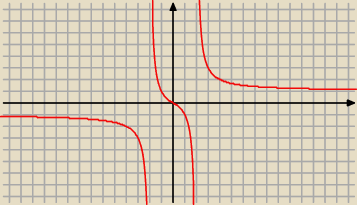
Adamm: widzimy z rysunku że funkcja przyjmuje wszystkie wartości rzeczywiste karty do gry, to żadne uzasadnienie

karty do gry : Dlaczego ? Ja w swoim rozumowaniu błędu nie widzę.

Adamm: no to jesteś ślepy

Adamm: rozumiem o co ci chodzi, następnym razem napisz że funkcja ciągła, więc przyjmuje wszystkie wartości z tego zakresu czy coś, a nie walisz nie wiadomo czym

kochanus_niepospolitus: bo nie masz błedu ... granice dobrze policzone i zgadzają się z wykresem funkcji

J.G.Darboux i jego twierdzenie: Panowie, nie kłócicie się! Nie ma o co.