Skracanie nawiasow Abcdef123: Czy mozna skracac nawiasy przy liczeniu asymptot poziomych i pionowych funkcji np (x+2)/(x+2)(x+3) czy mozna skrócić x+2? I jaka bedzie wtedy dziedzina?Prosze o odpowiedz tylko osob ktore sa pewne

yht: Kolejność: 1) dziedzina 2) skracanie 3) liczenie asymptot (z tego co pozostało po skracaniu) Ad. 1) x≠−2 oraz x≠−3 Ad. 2)

	1
pozostanie f(x) =
	x+3

asymptoty: poziome: lim_x→+∞ f(x) oraz lim_x→−∞ f(x), obie granice to 0 więc y=0 to asymptota pozioma obustronna pionowe:

	1
f(x) =
	x+3

x+3=0 x=−3 lim_x→−3⁺ f(x) = +∞ oraz lim_x→−3⁻ f(x) = −∞ stąd x=−3 jest asymptotą pionową obustronną

yht:

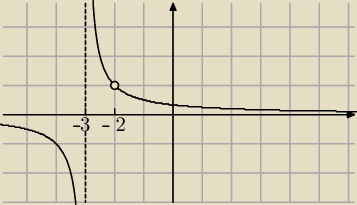
	x+2
wykres funkcji y =
	(x+2)(x+3)

yht:

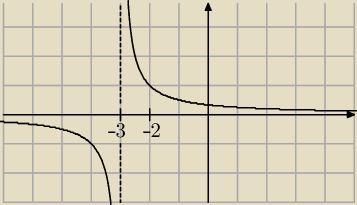
	1
dla porównania wykres funkcji y =
	x+3

123321:

	(x+2)
no ale w sumie pewien nie jestem bo		równie dobrze można zapisać jako
	(x+2)(x+3)

(x+2)(x+1000)
	i wykres teoretycznie powinien pozostac taki sam jezeli
(x+2)(x+3)(x+1000)

	2
obie strony przez to samo mnozymy bo to jest to samo tak samo jak		to to samo co
	5

	2*2
		,
	5*2

ale wychodzi ze dziedzina jest inna i w takim razie wykres tez jest inny... hmm

123321: ale skoro mowisz ze jest tak jak mowisz i nikt nie podwazyl, to pewnie tak jest

yht:

	(x+2)(x+1000)
wykres
	(x+2)(x+3)(x+1000)

będzie (prawie) taki sam co te powyższe − dojdzie "dziura" dla x=−1000