Styczne do okręgu
Czaffii: 3)Wyznacz równania stycznych do okręgu: (x−1)2+(y−2)2=8 poprowadzonych z punktu A(0,−3).
Oblicz pole czworokąta ABSC,gdzie B i C są punktami styczność, a S jest środkiem okręgu.
2 paź 19:10
Eta:
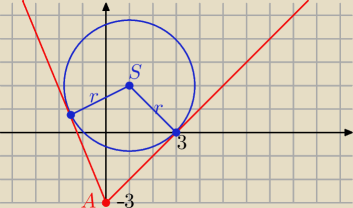
S(1,2) , r=2
√2
Styczne mają równanie
s: y=ax+b i A(0,−3)∊s
s: y=ax−3 ax−y−3=0 −−− równanie ogólne stycznych
Odległość d środka S od stycznych jest równa r
to:
|a−5|=2
√2*
√a2+1 /
2
a
2−10a+25=8a
2+8
7a
2+10a−17=0 Δ =576
√Δ=24
a=....= 1 v a= −17/7
styczne mają równania:
y=x−3 , y=(−17/7)x−3
========================
2 paź 19:49
Eta:
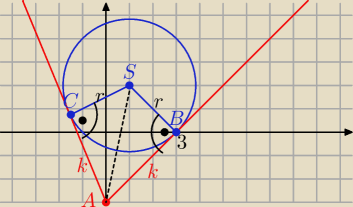
trójkąty ABS i ACS są przystające ( z tw. o odcinkach stycznych)
|AB|=|AC|=k= 3
√3 ( dł. przekątnej kwadratu o boku dł. 3
P(ABSC)= 2P(ΔABS) = r*k= .......
2 paź 20:00
Eta:
Rzucił zadania i czeka............ ( rano przepisze) i ma z głowy

2 paź 22:03
Czaffii: | | 1 | |
Nie nie. Policzyłem  |AS|= √26. P(ABSC)= |
| |CB|*|AS|. |
| | 2 | |
| | 1 | | 12 | |
|
| |CB|= |
| z wzoru na odległość punktu od prostej y=5x−3 |
| | 2 | | √26 | |
|AS|=
√26 z wzoru |AB|=
√(Xb−Xa)2+(Yb−Ya)2
No to P=12 j
2
Oczywiścię dziękuję za pomoc szczególnie w rozjaśnieniu umysłu

2 paź 22:43
Eta:
Teraz u siebie widzę chochlika
k=3√2
P(ABSC)=k*r= 3√2*2√2= 12 [j2]
2 paź 22:48
 S(1,2) , r=2√2
Styczne mają równanie s: y=ax+b i A(0,−3)∊s
s: y=ax−3 ax−y−3=0 −−− równanie ogólne stycznych
Odległość d środka S od stycznych jest równa r
to:
S(1,2) , r=2√2
Styczne mają równanie s: y=ax+b i A(0,−3)∊s
s: y=ax−3 ax−y−3=0 −−− równanie ogólne stycznych
Odległość d środka S od stycznych jest równa r
to:
 trójkąty ABS i ACS są przystające ( z tw. o odcinkach stycznych)
|AB|=|AC|=k= 3√3 ( dł. przekątnej kwadratu o boku dł. 3
P(ABSC)= 2P(ΔABS) = r*k= .......
trójkąty ABS i ACS są przystające ( z tw. o odcinkach stycznych)
|AB|=|AC|=k= 3√3 ( dł. przekątnej kwadratu o boku dł. 3
P(ABSC)= 2P(ΔABS) = r*k= .......

 |AS|=√26. P(ABSC)=
|AS|=√26. P(ABSC)=