Pole trójkąta w układzie współrzędnych Czaffii: 2) Pole powierzchni trójkąta ABC, gdzie A(0,4) B(3,0) wynosi 9(j²). Wyznacz współrzędne wierzchołka C, jeśli leży on na prostej 2x−y=0.

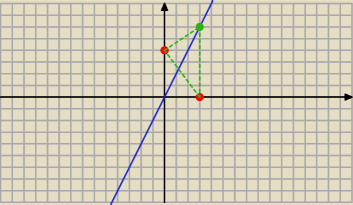
Adamm: C=(x; 2x) P=...=9 (jest na to wzór) koniec końców wyjdzie x=3

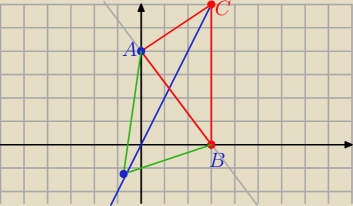
Janek191: C = ( x, 2 x) Prosta AB:

	4
a = −
	3

	4
y = −		x + b
	3

0 = − 4 + b ⇒ b = 4

	4
y = −		x + 4
	3

=================== I A B I = 5

	18
P = 0,5*5*h = 2,5 h = 9 ⇒ h =
	5

	18
Odległość punktu C od prostej AB jest równa h =
	5

3 y = − 4 x + 12 4 x + 3y − 12 = 0

	I 4*x + 3*2 x − 12I		18
h =		=
	5		5

I 10 x − 12 I = 18 x = 3 lub x = − 0, 6 y = 6 lub y = − 1,2 więc C = ( 3, 6) lub C = ( − 0,6 ; −1,2 ) ============================

Czaffii: Dzięki wielkie Janek191 za odpowiedź . Adamm wiem że ten wzór to

	1
Pabc=		|(Xb−Xa)(Yc−Ya)−(Yb−Ya)(Xc−Xa)|. Ale wynik mi wychodził C(3,6) lub C(−15,−30).
	2

Teraz zauważyłem błąd w postaci źle dodanych znaków minus i wynik wychodzi poprawnie. Dzięki za pomoc

Adamm: inny sposób v=[3 −4; 0], u=[x; 2x−4; 0] vxu=[0; 0; 10x−12] |vxu|=|10x−12|

1
	|vxu|=9
2

|10x−12|=18 x=3 lub x=−0,6

Janek191: @Adam Pewnie tego nie ma w liceum.

Adamm: wiem że nie ma, ale dla mnie tak jest prościej