Jednokładność
Czaffii: 1) Obrazem okręgu x2+y2−2x−6y+1=0 w pewnej jednokładności o skali dodatniej jest okrąg
x2+y2+16=8x+2y. Znajdź współrzędne środka tej jednokładności.
2 paź 19:05
piotr: x2+y2−2x−6y+1=0 ⇒ (x−1)2+(y−3)2 = 9 ⇒ r = 3
x2+y2+16=8x+2y ⇒ (x−4)2+(y−1)2 = 1 ⇒ R =1
skala = R/r = 1/3
środek: [1+(4−1)*3/4; 3+(1−3)*3/4] ⇒ [13/4; 3/2]
2 paź 20:27
Janek191:
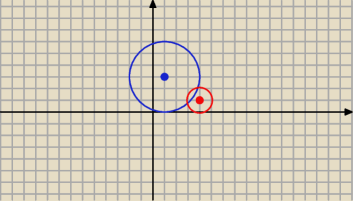
2 paź 20:39
Janek191:
Środek jednokładności pewnie źle policzony?

2 paź 20:41
piotr: środek jest OK
2 paź 20:47
Janek191:
Środki okręgów powinny być po tej samej stronie środka jednokładności. ( k > 0)
2 paź 20:53
piotr: no to będzie [4; 1/3]
2 paź 21:02
Janek191:
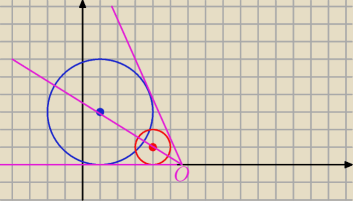
O = ( 5
12, 0)
===============
2 paź 21:17


 O = ( 512, 0)
===============
O = ( 512, 0)
===============