Funkcja homograficzna Placek: Cześć, mam problem z jednym zadaniem i mam nadzieję, że jeden z forumowiczów wytłumaczy mi jak je rozwiązać Dla jakich wartości parametru m równanie f(x)=m ma dokładnie dwa różne pierwiastki dodatnie:

	2|x−2|
a) f(x)=
	x+4

	|x−1|−|x−3|
b) f(x)=
	x−2

Będę wdzięczny za każdą okazaną pomoc, ponieważ nie wiem jak się wziąć za żaden z tych dwóch przykładów. Wiem, że można narysować i tak sprawdzić, ale nie wiem jak to się rysuje

Placek: Może jednak ktoś wie jak to zrobić ?

iteRacja: a/ najpierw zapisz bez wartości bezwzględnej analizujesz dwa przypadki − korzystasz z def. wartości bezwzględnej 1. x−2>=0 sprawdź jaką postać ma funkcja 2. x−2<0 i też sprawdź jaką postać ma funkcja napisz co wyszło z obliczeń

Mila: Piszę.

iteRacja: OK

Janek191:

	I 2 x − 4 I
a) f(x) =		x ≠ − 4
	x + 4

	4 − 2 x
1) Dla x < 2 i x ≠ − 4 mamy f(x) =
	x + 4

	2 x − 4
2) Dla x ≥ 2 i mamy f(x) =
	x + 4

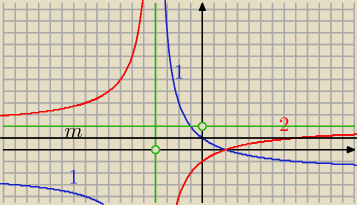
Rysujemy wykresy f w podanych przedziałach Z wykresu mamy Dla m ∊ ( 0 , 1) mamy dwa różne pierwiastki dodatnie.

Mila: Placek, jaką masz odpowiedź, bo ja albo Janek ma pomyłkę.

Janek191: Placka ktoś zjadł

Mila:

Mila: Ja mam chyba błąd, już szukam.

Janek191: Pierwiastki mają być dodatnie.

iteRacja: Mila przypadek 1/ rozwiązanie 4m+4=0 jest m=−1 a nie −4

Janek191: Hiperbola.

Mila: Znalazłam , dziękuję, nie piszę drugi raz. Najlepiej na kartce rozwiązać.

LWG: Tak jest. Nie tylko w TVN.

LWG: Jesteście wspaniali. Tak jest. To jest prawda. Muszę być grzeczny. Może moje nie być, ale nikt nie ucierpi przeze mnie.

Mila: x≠2 1) x<1

	−2
f(x)=−x+1−(−x+3)}{x−2}⇔f(x)=
	x−2

	−2
f(x)=		dla x<1
	x−2

2) x∊<1,3)

	x−1−(−x+3)		x−1+x−3
f(x)=		=
	x−2		x−2

	2x−4		2*(x−2)
f(x)=		=		=2 dla x≠2
	x−2		x−2

f(x)=2 dla x∊<1,3) 3) x≥3

	x−1−(x−3)		x−1−x+3
f(x)=		=
	x−2		x−2

	2
f(x)=
	x−2

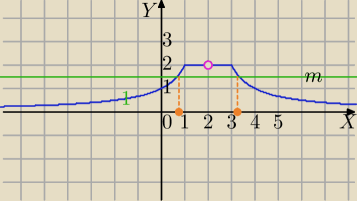
Równanie : f(x)=m ma dwa różne dodatnie rozwiązania dla m∊(1,2)

Mila: Witaj LWG. Masz wspaniały humor, to miło