Układy równań z wartością bezwzględna Kalirr: Witam. Mam problem ze zrozumieniem dlaczego przy rozwiązywaniu układu równań 3|x|+2y=1 2x−|y|=4 można to zrobić przez wyznaczenie x z drugiego równania i postawienia do pierwszego a w układzie |x|−y=1 − x+|y|=1 już tak się nie postępuje, e wyniku czego wychodzą przedziały w rozwiązaniu. Oba przykłady z książki a. Kiełbasy i oba mają inne rozwiązania

Adamm: to że tak nie robią, nie znaczy że tak nie można

Mila: |x|−y=1 − x+|y|=1 Taki układ?

Kalirr: Tak, taki układ. W tym drugim zrobiłem metodą postawienia i wyszło y=−1 i x=0. Nie wiem czy dobrze ale nawet jeśli to jak się zorientować, że to nie koniec zadania?

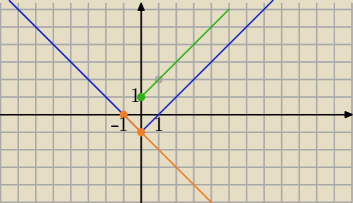
Mila: I sposób y=|x|−1 |y|=x+1 , x+1≥0⇔x≥−1 y≥0 to y=x+1 y<0 to y=−x−1 rozwiązanie : x∊<−1, 0> i y=−x−1 Algebraicznie: Za chwilę w nowym wpisie

Mila: Algebraicznie: |x|−y=1 − x+|y|=1 1) y≥0 ⇔|y|=y⇔−x+y=1,⇔y=x+1⇔x≥−1 |x|−x−1=1 |x|−x=2 a) X≥0 i y≥0 to równanie ma postać: x−x=2 brak rozwiązań b) x<0 ⇔|x|=−x −x−x=2 x=−1 i y=x+1⇔ x=−1 i y=0∊D 2) y<0⇔|y|=−y⇔y=−x−1 ⇔−x−1<0⇔x>−1 |x|+x+1=1⇔|x|+x=0 a) x≥0 i y<0 x+x=0 ⇔x=0 i y=−1 b) x<0 i y<0 −x+x=0 spełnione dla każdego x∊(−1,0) x∊(−1,0), y=−x−1 −−−−−−−−−−−−−−−−−−−−− odp. Sama napisz.