Prosta symetryczna względem punktu Zibi Kuźma: Wyznacz równanie prostej k, która jest obrazem prostej l: 4x −3y +5 = 0 w symetrii względem punktu B (−4, 5).

Ilona: 1.wyznacz dwa punkty należące do prostej l 2. wyznacz dla każdego punktu z osobna obraz w symetrii środkowej względem punktu B(−4,5) 3. napisz prostą przechodzącą przez wyznaczone obrazy punktów − to będzie prosta k

Jerzy: Albo: 1) prostopadła do k przez punkt B 2) punkt ich przecięcia A 3) punkt A' taki,że S jest środkiem AA' 4) równoległa do k przez punkt A'

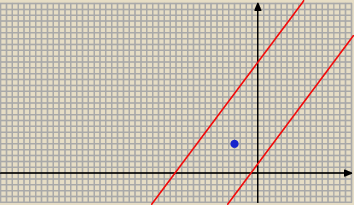
Adamm: przesuwamy płaszczyznę o wektor [4; −5] wtedy B znajdzie się w punkcie B'=(0; 0) nowe równanie prostej: 4(x−4)−3(y+5)+5=0 ⇔ 4x−3y−26=0 symetria względem (0; 0) 4(−x)−3(−y)−26=0 ⇔ 4x−3y+26=0 przesunięcie o wektor [−4; 5] 4(x+4)−3(y−5)+26=0 ⇔ 4x−3y+57=0

Adamm: inny sposób równanie prostej w symetrii względem tego punktu to 4x−3y+a=0 wystarczy by odległość tej prostej od punktu B była taka sama jak odległość l od B