wektory ciąg dalszy
studentzadyche: Jaki jest kąt między dwiema przekątnymi wewnętrznymi sześcianu? (Przekątna
wewnętrzna sześcianu łączy 2 wierzchołki i przechodzi przez środek sześcianu).
Wskazówka: Użyj iloczynu skalarnego wektorów.
Nawet nie wiem jak zaczać
1 paź 19:48
studentzadyche: Pewnie tak, że mam dwa wektory, jako dwie przekątne nazwijmy je a i b, wektory a i b są równej
długości więc |a|=|b|
1 paź 19:50
Mila:
Za godzinę narysuje.
1 paź 19:53
Jerzy:
Zastanów się jaką figurą jest przekrój zawierający te przekątne.
1 paź 19:54
Jerzy:
No.... to wytrzymaj jeszcze godzinę.
Witaj
Milu 
Robisz z grzybami ?
1 paź 19:55
studentzadyche: Jerzy, tylko to chodzi o przekątne wychodzące z wierzchołków naprzeciw siebie, czy
sąsiadujących, czy to kompletnie nie ma znaczenia ?
1 paź 19:56
studentzadyche:
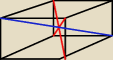
Chodzi tutaj o układ czerwona czerwona, czy na przykład czerwona niebieska, czy to może jednak
nie ma znaczenia
1 paź 19:59
Adamm: np. tak
niech sześcian będzie rozpięty na prostopadłych wektorach, a, b, c o długości d
v
1=a+b+c
druga to na przykład
v
2=−a+b+c
v
1•v
2=−d
2+d
2+d
2=d
2
|v
1|=
√d2+d2+d2, |v
2|=
√(−d)2+d2+d2
|v
1|*|v
2|=3d
2
v
1•v
2=|v
1|*|v
2|*cosα
1 paź 20:00
Adamm: wystarczy sobie to narysować, a jak ci lepiej, to narysuj w układzie współrzędnych
1 paź 20:01
kochanus_niepospolitus:
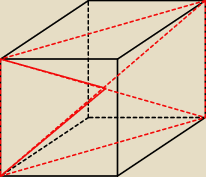
1 paź 20:12
Mila:
Cześć
Jerzy, grzybów nie jadam (poza pieczarkami).
Pozdrawiam

1 paź 20:16
kochanus_niepospolitus:
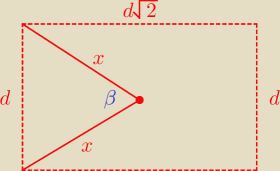
| | 1 | | √3 | |
x = |
| √d2 + 2d2 = |
| d |
| | 2 | | 2 | |
z tw. cosinusów:
| | 3 | | 1 | |
d2 = 2x2 − 2x2cosβ = 2x2(1−cosβ) = |
| d2(1−cosβ) ⇒ cosβ = |
| ⇒ β = arccos(1/3) |
| | 2 | | 3 | |
1 paź 20:16
studentzadyche: dziękuję

1 paź 20:39
 Robisz z grzybami ?
Robisz z grzybami ?
 Chodzi tutaj o układ czerwona czerwona, czy na przykład czerwona niebieska, czy to może jednak
nie ma znaczenia
Chodzi tutaj o układ czerwona czerwona, czy na przykład czerwona niebieska, czy to może jednak
nie ma znaczenia



