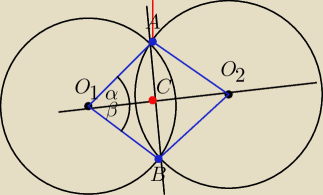
Wykazywanie 5-latek: Dwa okregi przecinaja sie w punktach A i B Wykazac ze ich wspolna cieciwa AB jest prostopadla do odcinka O₁O₂ laczacego srodki tych okregow Trojkaty O₁AO₂ i O₁BO₂ sa przystajace na podsatwie cechy BBB O₁A=O₁B jako promienie AO₂= B)₂ tez jako prpnienie O₁O₂ wspolny dla obu trojkatow Stad mam ze α=β W trojkacie AO₁B prosta O₁c jest dwusieczna kata przy wiecholku wiec jest prostopadla do podstawy z tego mam ze AB⊥O₁O₂

iteRacja: ΔAO₁B jest równoramienny (tak jak napisałeś O₁A = O₁B promienie) i dlatego dwusieczna kąta ∡AO₁B pokrywa się z wysokością poprowadzoną z wierzchołka O₁ (czyli O₁C) a jako wysokość jest prostopadła (z samego tego że jest dwusieczną nie wynika prostopadłość) O₁C ⊥ AB tak samo dla Δ AO₂B

5-latek: Czesc To znaczy mam napisane w ksiazce (przy trojkatach ze dwusieczna kata przy wiercholku trojkata jest jednoczesnie wysokoscia i srodkowa

iteRacja: nie w każdym trójkącie (i nie przy każdym wierzchołku) dwusieczna kąta pokrywa się z wysokością i środkową w podręczniku na pewno masz podane dla jakich przypadków się pokrywają

5-latek: iteRacja caly czas bylem myslami przy trojkacie rownoramiennym Takze w trojkacie rownobocznym

iteRacja: aha, jeśli nie chcesz korzystać z tej własności to można inaczej: Δ O₁CA i Δ O₂CB są przystające (bkb) stąd ∡O₁CA = ∡O₁CB wiemy że te kąty są przyległe: czyli ∡O₁CA + ∡O₁CB = 180^o a więc są proste: ∡O₁CA = ∡O₁CB = 90^o

iteRacja: to pamiętaj, że w trójkącie równoramiennym pokrywają się tylko dla kąta przy tym wierzchołku, w którym spotykają się równe ramiona