Jak ukazać że funkcja jest bijekcją konusisko: Jak matematycznym sposobem ukazać że funkcja jest bijekcją? Bo na pierwszy rzut oka widać iż funkcja poniżego linku jest bijekcją, ale jak to udowodnić matematycznie? Proszę o wytłumaczenie na przykładzie funkcji z poniższego linku https://image.ibb.co/djL5bG/qwqw.png

kochanus_niepospolitus: funkcja jest bijekcją jeżeli: ∀_x∊Df ∃{y∊{ZW} f(x) = y ∀_y∊ZW ∃_{x∊{D_f} f(x) = y ∀_x,z∊Df ∀_{y∊{ZW} f(x) = y ∧ f(z) = y ⇒ x = z ∀_x∊Df ∃_{y,z∊{ZW} f(x) = y ∧ f(x) = z ⇒ y = z i sprawdzasz czy wszystkie te warunki są spełnione

konusisko: umiem wykazać że funkcja jest injekcją: f(x₁)=f(x₂) 2x₁+3=2x₂+3 x₁=x₂ czyli jest injekcją ale jak wykazać na chłopski rozum że jest subjekcją?

kochanus_niepospolitus: a co jeśli x₁ = −1 albo x₁ = 0

konusisko: wtedy są wartości które funkcja x+3 nigdy nie przyjmie dla argumentów swojej dziedziny

konusisko: 2x+3 mi oczywiście chodziło

kochanus_niepospolitus: na chłopski rozum (to nie być 'po matematycznemu' ): funkcja g(x) = 2x+3 dla x∊R jest bijekcją, ponieważ mamy funkcję liniową o a≠0 funkcja f(x) spełnia warunek f(x) = g(x) dla prawie wszystkich x∊R, dla x=−1 g(x) = 1 ; f(x) = 3 dla x=0 g(x) = 3 ; f(x) = 1 czyli wartość f(−1) = g(0) ∧ f(0) = g(−1) jako, że g(x) jest bijekcją to wiemy, że nie istnieje żaden x₂ taki aby g(x₂) = 1 lub g(x₂) = 3 (o ile to nie jest x₂ = −1 bądź x₂ = 0) więc iniekcja jest spełniona także dla f(x) analogiczne rozumowanie dla suriekcji.

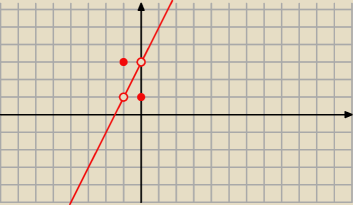
kochanus_niepospolitus: tak wygląda Twoja funkcja f(x)

konusisko: wiadomo że każda funkcja liniowa oprócz stałej jest Suriekcją

kochanus_niepospolitus: konusisko −−− i ja na tym opieram dalszy wywód. Pamiętaj jednak, że f(x) NIE JEST funkcją liniową g(x) nią jest

jc: Złożenie dwóch bijekcji jest bijekcją. h(x)=x dla x≠0,1 h(0)=−1 h(−1)=0 g(x) = 2x+3 f(x) = g(h(x))