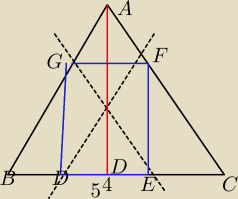
 W trojkat rownoramienny wpisano prostokat tak ze dwa jego wierzcholkileza na raminach AB I AC a
daw na podsatwie BC
Przekatne prostokata sa rownolegle do ramion trojkata
Obliczyc wysokosc AD widzac ze podstawa ma dlugosc 54cm a obwod prostokata = 84cm
W trojkat rownoramienny wpisano prostokat tak ze dwa jego wierzcholkileza na raminach AB I AC a
daw na podsatwie BC
Przekatne prostokata sa rownolegle do ramion trojkata
Obliczyc wysokosc AD widzac ze podstawa ma dlugosc 54cm a obwod prostokata = 84cm
 odobienstwa bo tego jescze nie
mialem
Bylo natomiast linie srodkowe trojkata i trapezu , dwie proste przeciete sieczna .
odobienstwa bo tego jescze nie
mialem
Bylo natomiast linie srodkowe trojkata i trapezu , dwie proste przeciete sieczna .

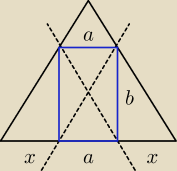 2x+a = 54
2(a+b) = 84
x = a <−−−− wynika z tego, że ECFG jest równoległobokiem
2x+a = 54
2(a+b) = 84
x = a <−−−− wynika z tego, że ECFG jest równoległobokiem 
 Stąd masz, że GECF jest równoległobokiem, więc GE=FC i GF=EC
Stąd masz, że GECF jest równoległobokiem, więc GE=FC i GF=EC
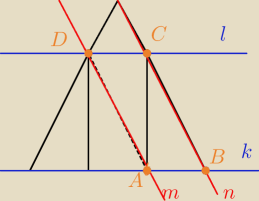 m||n −−− z treści zadania to wynika
k||l −−− to wynika z tego, że te proste zawierają dwa przeciwległe boki prostokąta
zgoda
m||n −−− z treści zadania to wynika
k||l −−− to wynika z tego, że te proste zawierają dwa przeciwległe boki prostokąta
zgoda No to mamy:
1) ABCD jest czworokątem, który posiada cztery boki, po dwa równoległe do siebie
No to mamy:
1) ABCD jest czworokątem, który posiada cztery boki, po dwa równoległe do siebie  2) Skoro ma taką zależność to jest to równoległobok.
3) Skoro jest równoległobokiem to |AB| = |DC|
2) Skoro ma taką zależność to jest to równoległobok.
3) Skoro jest równoległobokiem to |AB| = |DC|
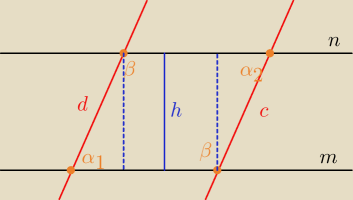 Z twierdzenia 'jakiegoś tam' odnośnie kątów prostej przeciętej prostymi równoległymi: α1 = α2
Niech h oznacza odległość pomiędzy prostymi.
Skoro m||n to h = const.
Skoro h = const. to z trygonometrii:
Z twierdzenia 'jakiegoś tam' odnośnie kątów prostej przeciętej prostymi równoległymi: α1 = α2
Niech h oznacza odległość pomiędzy prostymi.
Skoro m||n to h = const.
Skoro h = const. to z trygonometrii:
| h | ||
sin α1 = | ||
| d |
| h | ||
sin α2 = | ||
| c |
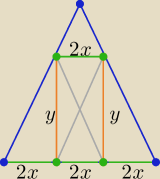 Witam
Witam  1/ rysunek i odpowiednie oznaczenia zgodne z treścią zadania
2/ 6x=54 ⇒ x=9
3/ 4x+2y=84 ⇒ ......... y=24
1/ rysunek i odpowiednie oznaczenia zgodne z treścią zadania
2/ 6x=54 ⇒ x=9
3/ 4x+2y=84 ⇒ ......... y=24
| b | wysokość trójkąta | |||
tg(kąt przy podstawie dużego trójkąta) = | = | |||
| a | połowa podstawy |
| 3 | ||
zauważyć, że wysokość trójkąta = | b ... ponieważ: | |
| 2 |
| 1 | ||
stąd wniosek: x = | b | |
| 2 |
| |AD| | 3x | 3 | |||
= | ⇒ ....... |AD|= | *24=36 | |||
| y | 2x | 2 |
 Bo jeszcze go nie przerabiał
Bo jeszcze go nie przerabiał  I w tym cała trudność
I w tym cała trudność 
 Może chce jechać z Gdańska do Sopotu przez Londyn?
No to niech jedzie.........
Może chce jechać z Gdańska do Sopotu przez Londyn?
No to niech jedzie......... 
 Tutaj nie chodzi o to zeby przerobic bo to zrobie w odpowiednim czasie
Dotad byly Podsatwowe utwory i pojecia geometryczne
Trojkaty .tzn cechy przystawania , zaleznosc miedzy bokami i kątami w trohkacie . Duzo o
trojkatach rownoramiennych (dwusieczna itd
Jestem przy rozdziale trzecim w ksiazce do geometrii i zadanie jest z tego rozdzialu (no
chyba ze cos nalezalo pamietac z eszkoly podsytwowej
mam tam Proste rownolegle
Twierdzenie proste i odwrotne o katach odpowiadajacych
Suma katow wewnetrzych trojkata Twierdzenie o kącie zewnetrzym
Katy o ramionach odpowiednio prostopadlych
Rownolegloboki i ich wlasnosci
Twierdzenie o rownoleglych wyznaczajace na jednym ramieniu kąta rowne odcinki
(MOz e ztego nalezalo skorzystac w tym zadaniu )
Odcinek lacacy srodki bokow trojkata ,. Srodek ciezkosci trojkata Trapez (tez linia srodkowa
Podstawowe zadania konstrukcyjne (to nie przerobilem dokladnie )
Ksiazka nie jest z tych czasow lecz z 61r i podzielona jest na lekcje (w sumie 49 )
To oczym piszecie bedzie w rozdziale 8 i 9 .Wiec daleko do tego
Tutaj nie chodzi o to zeby przerobic bo to zrobie w odpowiednim czasie
Dotad byly Podsatwowe utwory i pojecia geometryczne
Trojkaty .tzn cechy przystawania , zaleznosc miedzy bokami i kątami w trohkacie . Duzo o
trojkatach rownoramiennych (dwusieczna itd
Jestem przy rozdziale trzecim w ksiazce do geometrii i zadanie jest z tego rozdzialu (no
chyba ze cos nalezalo pamietac z eszkoly podsytwowej
mam tam Proste rownolegle
Twierdzenie proste i odwrotne o katach odpowiadajacych
Suma katow wewnetrzych trojkata Twierdzenie o kącie zewnetrzym
Katy o ramionach odpowiednio prostopadlych
Rownolegloboki i ich wlasnosci
Twierdzenie o rownoleglych wyznaczajace na jednym ramieniu kąta rowne odcinki
(MOz e ztego nalezalo skorzystac w tym zadaniu )
Odcinek lacacy srodki bokow trojkata ,. Srodek ciezkosci trojkata Trapez (tez linia srodkowa
Podstawowe zadania konstrukcyjne (to nie przerobilem dokladnie )
Ksiazka nie jest z tych czasow lecz z 61r i podzielona jest na lekcje (w sumie 49 )
To oczym piszecie bedzie w rozdziale 8 i 9 .Wiec daleko do tego