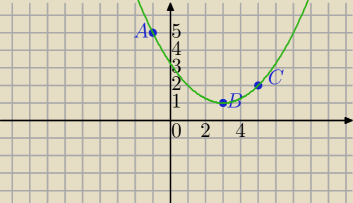
Wyznacz wzór funkcji kwadratowej, wiedząc że do jej wykresu należą punkty... j77: Wyznacz wzór funkcji kwadratowej, wiedząc że do jej wykresu należą punkty: A = (−1, 5) B = (3, 1) C = (5, 2) Podstawiam to pod wzór funkcji kwadratowej: 5 = a − b + c 1 = 9a + 3b + c 2 = 25a + 5b + c Ale gdy próbuję to rozwiązać to wychodzą strasznie dziwne liczby, jak poprawnie rozwiązać taki układ równań?

Blee: To pokaz jak liczysz

Blee: Bez liczenia zgaduje ze: a = 0.5 x_wierzcholka = 3 y_wierzcholka = 1 Czyli punkt B jest wierzcholkiem.

Blee: Więc mamy f(x) = 0.5(x−3)² + 1

5-latek: Czesc Blee Mozna rozwiazac tak 1 Wzor interpolacyjny Lagrange"a (nie ma go w liceum 2) metoda wyznacznikowa (wyznacznik stopnia trzeciego ,, nie weim czy go Wam pokazywali jak rozwiazaywac 3. Np z 1 rownania wyznaczyc jaks zmienna i podstawiac .

5-latek: Czesc Blee Mozna rozwiazac tak 1 Wzor interpolacyjny Lagrange"a (nie ma go w liceum 2) metoda wyznacznikowa (wyznacznik stopnia trzeciego ,, nie weim czy go Wam pokazywali jak rozwiazaywac 3. Np z 1 rownania wyznaczyc jaks zmienna i podstawiac .

Blee: Cos nie tak zapisalem

Blee: To bedzie: f(x) = 0.25(x−3)² + 1 Witam 5−latka

j77: Nie chodzi mi o sam wzór funkcji bo on mi nie powie jak to zrobić, tylko jak to obliczyć, tak jak mówił 5−latek: podstawianiem pod równanie

kochanus_niepospolitus: dlatego na początku napisałem −−− POKAŻ SWOJE OBLICZENIA

Adamm: 1, −1, 1, 5 9, 3, 1, 1 25, 5, 1, 2 w₂ → w₂−w₁ w₃ → w₃−w₁ 1, −1, 1, 5 8, 4, 0, −4 24, 6, 0, −3 w₂ → w₂/4 w₃ → w₃/3 1, −1, 1, 5 2, 1, 0, −1 8, 2, 0, −1 w₃ → w₃−2w₂ w₃ → w₃/4 1, −1, 1, 5 2, 1, 0, −1 1, 0, 0, 1/4 w₂ → w₂−2w₁ w₁ → w₁−w₃ 0, −1, 1, 19/4 0, 1, 0, −3/2 1, 0, 0, 1/4 w₁ → w₁+w₂ 0, 0, 1, 13/4 0, 1, 0, −3/2 1, 0, 0, 1/4 no i mamy a=1/4, b=−3/2, c=13/4 f(x)=(1/4)x²−(3/2)x+13/4=(1/4)(x−3)²+1

Mila: 5 = a − b + c 1 = 9a + 3b + c 2 = 25a + 5b + c (1−2), (2−3) 4=−8a−4b /:(−2) −1=−16a−2b −−−−−−−−−−−− 4a+2b=−2 −16a−2b=−1 −−−−−−−− + −12a=−3

	1		3
a=		⇔2b=−2−4a , 2b=−2−1, b=−
	4		2

	1		3
5=		+		+c
	4		2

	7		13
c=5−		⇔ c=
	4		4

	1		3		13
f(x)=		x2−		x+
	4		2		4

j77: Dziękuję

Eta: Umieszczając punkty w układzie współrzędnych W=B(3,1) Z postaci kanonicznej y=a(x−3)²+1 i C(5,2) i A(−1,5) 2=a(5−3)²+1 5=a(−1−3)²+1 2=4a+1 5=16a+1

	1		1
a=		a=
	4		4

	1
y=		(x−3)2+1 −− postać kanoniczna
	4

	1		3		13
y =		x2−		x+		−− postać ogólna
	4		2		4